
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,其中正确的结论有( )个.
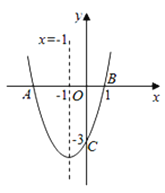
A. 3B. 4C. 2D. 1
【答案】A
【解析】
利用抛物线的对称性可确定A点坐标为(-3,0),则可对①进行判断;利用判别式的意义和抛物线与x轴有2个交点可对②进行判断;由抛物线开口向下得到a>0,再利用对称轴方程得到b=2a>0,则可对③进行判断;利用x=-1时,y<0,即a-b+c<0和a>0可对④进行判断.
∵抛物线的对称轴为直线x=-1,点B的坐标为(1,0),
∴A(-3,0),
∴AB=1-(-3)=4,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a>0,
∵抛物线的对称轴为直线x=-![]() =-1,
=-1,
∴b=2a>0,
∴ab>0,所以③错误;
∵x=-1时,y<0,
∴a-b+c<0,
而a>0,
∴a(a-b+c)<0,所以④正确.
故选A.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,顶点
两点,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
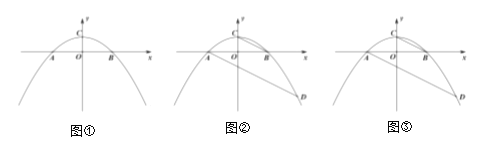
(1)如图①,求抛物线的解析式;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在第四象限的抛物线上,过点
在第四象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省十堰市,第24题,10分)已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
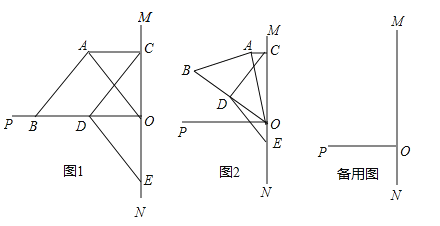
(1)如图1,若点B在OP上,则:
①AC OE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是 ;
(2)将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
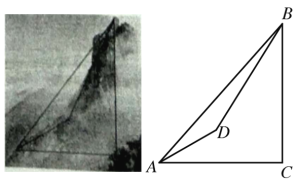
【题目】某学校数学兴趣小组想利用数学知识测量某座山的海拔高度,如图,他们在山腰A处测得山顶B的仰角为45°,他们从A处沿着坡度为i=1 : ![]() 的斜坡前进1000 m到达D处,在D处测得山顶B的仰角为58°,若点A处的海拔为12米,求该座山顶点B处的海拔高度,(结果保留整数,参考数据:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,
的斜坡前进1000 m到达D处,在D处测得山顶B的仰角为58°,若点A处的海拔为12米,求该座山顶点B处的海拔高度,(结果保留整数,参考数据:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,![]() ≈1. 732)
≈1. 732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某班“讲故事”比赛中有一个抽奖活动,活动规则是:只有进入最后决赛的甲、乙、丙三位同学,每人才能获得一次抽奖机会.在如图所示的翻奖牌正面的4个数字中选一个数字,选中后就可以得到该数字后面的相应奖品:前面的人选中的数字,后面的人就不能再选择数字了.
(1)请用树状图(或列表)的方法求甲、乙二人得到的奖品都是计算器的概率.
(2)有的同学认为,如果甲先翻奖牌,那么他得到篮球的概率会大些,这种说法正确吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
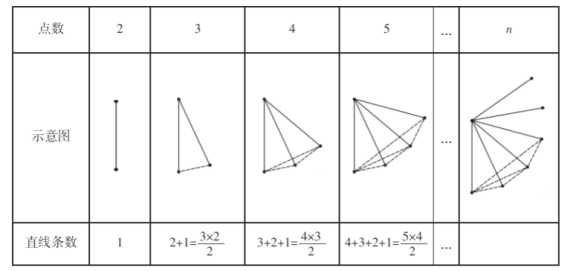
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交舡于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2) 求证: ![]() ;
;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
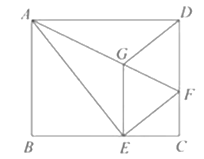
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com