
����Ŀ����ij��������������������һ���齱���������ǣ�ֻ�н����������ļס��ҡ�����λͬѧ��ÿ�˲��ܻ��һ�γ齱����������ͼ��ʾ�ķ����������4��������ѡһ�����֣�ѡ�к�Ϳ��Եõ������ֺ������Ӧ��Ʒ��ǰ�����ѡ�е����֣�������˾Ͳ�����ѡ����������
��1��������״ͼ�����б����ķ�����ס��Ҷ��˵õ��Ľ�Ʒ���Ǽ������ĸ�����
��2���е�ͬѧ��Ϊ��������ȷ����ƣ���ô���õ�����ĸ��ʻ��Щ������˵����ȷ����˵��������

���𰸡���1��![]() ����2������˵���Dz���ȷ�������ɼ�������
����2������˵���Dz���ȷ�������ɼ�������
��������
�����������1�����Ȼ�����ͼ��֪��һ����24��������ס��Ҷ��˶��õ�����������2������������������Ϊ������ʣ�
��2�����ݣ�1���е�����ͼ���ֱ�����ס��ҡ����õ�����ĸ��ʼ�����
�����������1�����л��������״ͼ���£�

����24�ֿ��ܵ���������мס��Ҷ��˶��õ�����������4�������
���ԣ��ס��Ҷ��˶��ü������ĸ���Ϊ��P=![]() ��
��
��2������˵���Dz���ȷ�������������״ͼ��֪����24�ֿ��������
�õ����������ֿ��������P���ף�=![]() ��
��
�ҵõ����������ֿ��������P���ң�=![]() ��
��
���õ����������ֿ��������P������=![]() ��
��
���Լס��ҡ������˲���˭�ȷ����Ƶõ�����ĸ��ʶ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ķ���A��C�ֱ���
�Ķ���A��C�ֱ���![]() ��
��![]() ���������ϣ�����������
���������ϣ�����������![]() ��
��![]() �������
�������![]() �ı�AB��BC���ڵ�D��E��
�ı�AB��BC���ڵ�D��E��

��1����![]() ����
����![]() �����Ϊ_________��
�����Ϊ_________��
��2����DΪAB���е㣮
����֤��EΪBC���е㣻
����![]() �����Ϊ4����
�����Ϊ4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=5cm����ADC=120������E��Fͬʱ��A��C����������ֱ���AB��CB�������B�����ƶ�(����BΪֹ)����E���ٶ�Ϊ1cm/s����F���ٶ�Ϊ2cm/s������t���DEFΪ�ȱ������Σ���t��ֵΪ(����)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�Ĵ������
1����![]() ��8.9����7��
��8.9����7�� ![]() ����3.2��+1 008����0.06��28����9��
����3.2��+1 008����0.06��28����9��
���������ϣ�{______��}��
���������ϣ�{______��}��
���������ϣ�{______��}��
���������ϣ�{______��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵�������װ�ޣ�����ס�������װ��ͬʱʩ����8����ɣ��踶���ӹ�3520Ԫ���ã�������ӵ�����6�죬�����Ҷӵ�����12�������ɣ��踶���ӹ�3480Ԫ���á�
(1)�ס������ӹ���һ�죬�̳���Ӧ������Ԫ?
(2)�������ĸ���װ�ޣ��̳�������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ��ڹ涨ʱ��������24000�����������������ͻȻ���蹩��������ʵ�ʹ���Ч�ʱ�ԭ�ƻ������50%������ǰ5������������������������ù���ԭ�ƻ�ÿ��ӹ�����������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���⣺��֪����ͼ,![]() ,
,![]() .��֤��
.��֤��![]() .
.
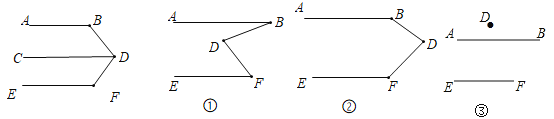
��ʦҪ��ѧ�����������̲��ϵ���Ŀ֤�����Զ�ͼ�ν��б��Σ���������չ̽����������ʲô�·��֣�
��1��Сӱ��������˶�������֤������֤�����������õ���ƽ���ߵ�һ�����ʣ�Сӱ�õ���ƽ�������ʿ����� .
��2����������Сӱ�á����λ��塷��ͼ�ν����˱�ʽ�����Ȼ�������ƽ����![]() ��Ȼ����ƽ���仭��һ��
��Ȼ����ƽ���仭��һ��![]() ������
������![]() ��������϶���
��������϶���![]() ���ֱ�õ���ͼ
���ֱ�õ���ͼ![]()
![]() ��Сӱ����ͼ
��Сӱ����ͼ![]() ����������Ŀ��ԭ�ͣ�������������Ľ��۲��뵽ͼ
����������Ŀ��ԭ�ͣ�������������Ľ��۲��뵽ͼ![]() ��
��![]() ͼ�е���
ͼ�е���![]() ֮��Ҳ���ܴ�����ij��������ϵ.���������á����λ��塷�Ķ�������㹦�ܣ��ҵ�����������֮���������ϵ.
֮��Ҳ���ܴ�����ij��������ϵ.���������á����λ��塷�Ķ�������㹦�ܣ��ҵ�����������֮���������ϵ.
������Сӱ����̽���Ļ����ϣ����������������⣺
����������ͼ![]() ��
��![]() ��
��![]() ֮���������ϵ������֤����
֮���������ϵ������֤����
��������ȫͼ![]() ��ֱ��д��
��ֱ��д��![]() ��
��![]() ֮���������ϵ�� .
֮���������ϵ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABC�У���ABC���ACB��ƽ�����ཻ�ڵ�P��
��1�������A=80��������BPC�Ķ�����
��2����ͼ�ڣ�����ABC�����MBC����NCB�Ľ�ƽ���߽��ڵ�Q����̽����Q����A֮���������ϵ��
��3����ͼ�ۣ��ӳ��߶�BP��QC���ڵ�E����BQE�У�����һ���ڽǵ�����һ���ڽǵ�2��������A�Ķ���.


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com