
����Ŀ��ij������ó��˾��������50�����г���������������Ϊÿ��ÿ��200Ԫʱ��ȫ������������ÿ���10Ԫ�����ȥ�ij��ͼ���2����
��1���������߶���Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2����˾�쵼ϣ��������ﵽ10160Ԫ������Ϊ�ܷ�ʵ�֣����ܣ������ʱ����������ܣ���˵�����ɣ�
��3�������ճ�ά��Ҫ�����ã���֪�����ÿ��ά����Ϊ100Ԫδ����ij���ά����Ϊ50Ԫ�������Ϊ����Ԫʱ����˾������ǡ��Ϊ5500Ԫ�����������橁ά���ѣ�
���𰸡���1����������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ����2�������治�ܴﵽ10160Ԫ�����ɼ���������3�������Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��
��������
��1����������xԪ����ÿ�տ������50��![]() ��������������=ÿ������������з��̼��ɵô𰸣���2��������ʵ�֣���������=ÿ������������ɵ�һԪ���η��̣����ݸ����б�ʽ���ɵô𰸣���3����������xԪ�������������橁ά������һԪ���η��̣������xֵ�������ɵ����.
��������������=ÿ������������з��̼��ɵô𰸣���2��������ʵ�֣���������=ÿ������������ɵ�һԪ���η��̣����ݸ����б�ʽ���ɵô𰸣���3����������xԪ�������������橁ά������һԪ���η��̣������xֵ�������ɵ����.
��1����������xԪ����ÿ�տ������50��![]() ������
������
�����⣬�ã���200+x����50��![]() ����10120��
����10120��
�������ã�x2��50x+600��0��
��ã�x1��20��x2��30��
�𣺵�������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2��������ʵ�֣�������xԪ��
�����⣬�ã���200+x����50��![]() ����10160��
����10160��
�������ã�x2��50x+900��0��
�ߡ�������50��2��4��1��900��0��
���һԪ���η����⣬
�������治�ܴﵽ10160Ԫ��
��3����������xԪ��
�����⣬�ã���200+x����50��![]() ����100��50��
����100��50��![]() ����50��
����50��![]() ��5500��
��5500��
�������ã�x2��100x+2500��0��
��ã�x1��x2��50��
��200+x��250��
�𣺵����Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
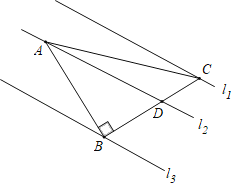
����Ŀ����ͼ������ABC�У���ABC��90����AB��BC�������εĶ������ƽ�е�����ֱ��l1��l2��l3�ϣ���l1��l2֮��ľ���Ϊ2��l2��l3֮��ľ���Ϊ3��BC��l2��D�㣮
��1����AB�ij���
��2����sin��BAD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ��������˳���Ĺ��������������ƻ��Գ�����·�����˸��죬�ְ��żס����������̶���ɣ���֪�ӵĹ���Ч�����Ҷӹ���Ч�ʵ�![]() �����Ӹ���360�ĵ�·���ҶӸ���ͬ�����ĵ�·����3�죮
�����Ӹ���360�ĵ�·���ҶӸ���ͬ�����ĵ�·����3�죮
��1���ס��������̶�ÿ���ܸ����·�ij��ȷֱ��Ƕ����ף�
��2�����ӹ���һ���踶����7��Ԫ���Ҷӹ���һ���踶����5��Ԫ���������ĵ�·ȫ��1200�ף������ܷ��ò�����145��Ԫ�����ٰ��żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�߳�ABΪ4�ľ���ֽƬ�۵���ʹ��D���B�غϣ��ۺ�ΪEF����EF��2![]() ������ε����Ϊ��������
�����������������
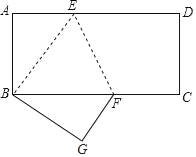
A.32B.28C.30D.36
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
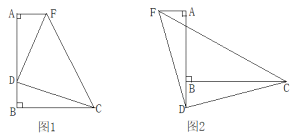
����Ŀ����֪��ABC=90�㣬D��ֱ��AB���ϵĵ㣬AD=BC
��1����ͼ1����D���߶�AB�ϣ�����A��AF��AB����AF=BD������DC��DF��CF�����жϡ�CDF����״��˵�����ɣ�
��2����ͼ2����D���߶�AB���ӳ����ϣ���F�ڵ�A����࣬�����������䣬���Ͻ����Ƿ���Ȼ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
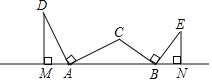
����Ŀ����ͼ���ڡ�ABC�У���ACBΪ�۽ǣ��ѱ�AC�Ƶ�A����ʱ�뷽����ת90���AD���ѱ�BC�Ƶ�B��˳ʱ�뷽����ת90���BE����DM��AB�ڵ�M��EN��AB�ڵ�N����AB��5��EN��2����DM��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�ڽ���Բ����D���ӻ�![]() �ϣ�AD��
�ϣ�AD��![]() BC��DC��
BC��DC��![]() AB��QΪAC�е㣬��D���P���ڵ�Q�Գƣ�
AB��QΪAC�е㣬��D���P���ڵ�Q�Գƣ�
��1����֤����PAD�ס�ABC��
��2����֤����B��P��D��һ��ֱ���ϣ�
��3����ͼ2���ǡ�PAB��������PCB��������ABC���������ú��������Ĵ���ʽ��ʾ����
��4����ͼ3����E��F�ֱ�ΪAB��BC���е㣬EF��BD�ڵ�H����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
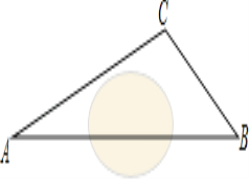
����Ŀ����һ�ο���ʵ����У�ͬѧ��Ҫ����ij���˹�������A��B������֮ͤ��ľ��룮ѡ��ͤA��C��Ϊ�۲�㣮��ͼ���ֲ�á�CAB��45������ACB��98����AC��200�ף������A��B������֮ͤ��ľ��롢�������ȷ��1�ף����ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��sin 37���0.6��cos 37���0.8��tan 37���0.75��
��1.732��sin 37���0.6��cos 37���0.8��tan 37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����о��ü���������ij�����ֻ�����˾�ӵ�����300�������ֻ��Ķ�����Ϊ�˾��콻����������һ�������ߣ�ʵ��ÿ������������ԭ�ƻ������50%�������ԭ�ƻ���ǰ5������ɽ�������ÿ��ʵ�����������ֻ�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com