
【题目】如图1,△ABC内接于圆,点D在劣弧![]() 上,AD=
上,AD=![]() BC,DC=
BC,DC=![]() AB,Q为AC中点,点D与点P关于点Q对称.
AB,Q为AC中点,点D与点P关于点Q对称.
(1)求证:△PAD∽△ABC.
(2)求证:点B,P,D在一条直线上.
(3)如图2,记∠PAB=α,∠PCB=β,∠ABC=θ,请用含α,β的代数式表示θ.
(4)如图3,设E,F分别为AB,BC的中点,EF交BD于点H,求![]() 的值.
的值.

【答案】(1)详见解析;(2)详见解析;(3)θ=90°﹣![]() ﹣
﹣![]() ;(4)
;(4)![]()
【解析】
(1)由对角线互相平分的四边形是平行四边形可证四边形APCD是平行四边形,可得AP=CD,AP∥CD,可证∠PAD=∠B,即可证△PAD∽△ABC;
(2)由相似三角形的性质可得∠ACB=∠ADP,又由∠ACB=∠ADB,可得∠ADP=∠ADB,可证点B,P,D在一条直线上;
(3)由外角性质可得∠APD+∠CPD=∠ABP+∠BAP+∠CBP+∠PCB=α+β+θ,由平行四边形的性质和圆的内接四边形的性质可得180°﹣∠ABC=α+β+θ,即可求解;
(4)根据题意连接EP,FP,由角的数量关系可求∠EPF=90°,通过相似三角形的判定和性质可证EH=HF,由直角三角形的性质可求PH=![]() EF=
EF=![]() AC,即可求解.
AC,即可求解.
解:(1)∵点Q为AC中点,点D与点P关于点Q对称,
∴AQ=QC,PQ=QD,
∴四边形APCD是平行四边形,
∴AP=CD,AP∥CD,
∴∠PAD+∠ADC=180°,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠PAD=∠B,
又∵![]() ,
,
∴△PAD∽△ABC.
(2)连接BD,如图2,
∵△PAD∽△ABC,
∴∠ACB=∠ADP,
∵∠ACB=∠ADB,
∴∠ADP=∠ADB
∴点B,P,D在一条直线上.
(3)∵∠APD=∠ABP+∠BAP,∠CPD=∠CBP+∠PCB,
∴∠APD+∠CPD=∠ABP+∠BAP+∠CBP+∠PCB=α+β+θ,
∵四边形APCD是平行四边形,
∴∠ADC=∠APC=∠APD+∠CPD,
∴180°﹣∠ABC=α+β+θ,
∴2θ=180°﹣α﹣β,
∴θ=90°﹣![]() ﹣
﹣![]() .
.
(4)连接EP,FP,
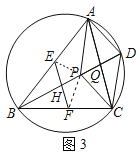
∵E,F分别为AB,BC的中点,
∴AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,
BC,
∵CD=![]() AB,CD=AP,
AB,CD=AP,
∴AE=AP,
∴∠APE=90°﹣![]() α,
α,
同理可得∠CPF=90°﹣![]() β,
β,
∴∠EPF=360°﹣∠APE﹣∠CPF﹣∠APC=180°﹣(![]() α+
α+![]() β+θ),
β+θ),
∵θ=90°﹣![]() ﹣
﹣![]() ,
,
∴∠EPF=180°﹣(![]() α+
α+![]() β+90°﹣
β+90°﹣![]() ﹣
﹣![]() )=90°,
)=90°,
∵E是AB的中点,点F是BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
∴△BEH∽△BAQ,△BFH∽△BCQ,
∴![]() ,
,
∵AQ=CQ,
∴EH=HF,
∴PH=![]() EF=
EF=![]() AC,
AC,
∴![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是 (填A或B).
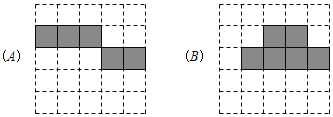
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)

(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
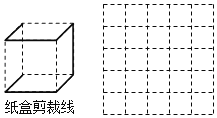
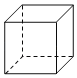
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中为了提高学生综合素质,决定开设以下校本课程:![]() .软笔书法,
.软笔书法,![]() .经典诵读,
.经典诵读,![]() .钢笔画,
.钢笔画,![]() .花样跳绳,为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行了调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
.花样跳绳,为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行了调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
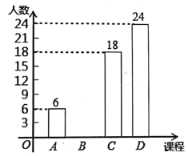
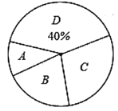
(1)这次被调查的学生共_____人;
(2)请将条形统计补充完整;
(3)在平时的花样跳绳的课堂学习中,甲、乙、丙三人表现优秀,现决定从这三名同学中任选两名参加全区综合素质展示,求恰好同时选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租贸公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10160元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由,
(3)汽车日常维护要定费用,已知外租车辆每日维护费为100元未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益﹣维护费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,B(5,0),点A在第一象限,且OA=OB,sin∠AOB=![]() .
.
(1)求过点O,A,B三点的抛物线的解析式.
(2)若y=![]() 的图象过(1)中的抛物线的顶点,求k的值.
的图象过(1)中的抛物线的顶点,求k的值.
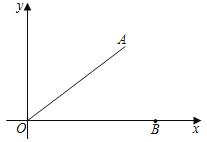
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
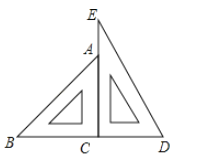
【题目】一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺ABC绕着点C按逆时针方向旋转n°后(0<n<360 ),若ED⊥AB,则n的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过A(n,b),B(m,a)且m+n=1.
(1)当b=a时,直接写出函数图象的对称轴;
(2)求b和c(用只含字母a、n的代数式表示):
(3)当a<0时,函数有最大值-1,b+c≥a,n≤![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com