
【题目】如图,在平面直角坐标系中,B(5,0),点A在第一象限,且OA=OB,sin∠AOB=![]() .
.
(1)求过点O,A,B三点的抛物线的解析式.
(2)若y=![]() 的图象过(1)中的抛物线的顶点,求k的值.
的图象过(1)中的抛物线的顶点,求k的值.
科目:初中数学 来源: 题型:
【题目】已知等腰直角△ABC,∠C=90°,AC=2,D为边AC上一动点,连结BD,在射线BD上取一点E使BEBD=AB2.若点D由A运动到C,则点E运动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
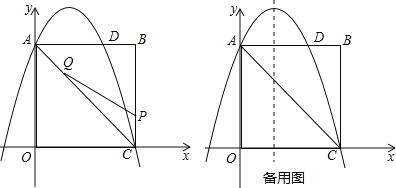
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
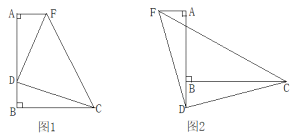
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于圆,点D在劣弧![]() 上,AD=
上,AD=![]() BC,DC=
BC,DC=![]() AB,Q为AC中点,点D与点P关于点Q对称.
AB,Q为AC中点,点D与点P关于点Q对称.
(1)求证:△PAD∽△ABC.
(2)求证:点B,P,D在一条直线上.
(3)如图2,记∠PAB=α,∠PCB=β,∠ABC=θ,请用含α,β的代数式表示θ.
(4)如图3,设E,F分别为AB,BC的中点,EF交BD于点H,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
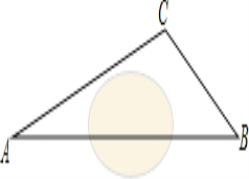
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小伟一起参加象棋比赛,他们所在的小组共有5名选手.抽签袋里有2红2黑1白共5个小球,摸到同色的成为首轮对手,摸到白球的首轮轮空.现在小组其他3名选手首先依次各摸走一个小球,小亮看到第1个选手摸走的是红球,他对小伟说根据这3名选手的摸球结果我已经知道咱俩恰好首轮对阵的概率了.请你求这个概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
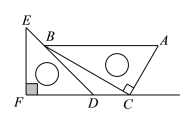
【题目】将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,∠F=∠ACB=90°,AB∥CF,∠E=45°,∠A=60°,AC=8,则CD的长度是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com