
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
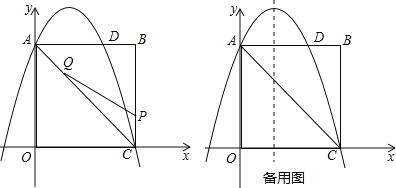
(1)求抛物线的函数解析式;
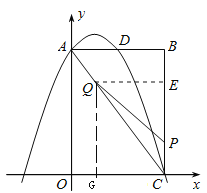
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+8;(2)①S=﹣
x+8;(2)①S=﹣![]() m2+3m;②满足条件的点F共有四个,坐标分别为F1(
m2+3m;②满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).
【解析】
(1)将A、C两点坐标代入抛物线y=![]() x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数;
②先求出m=5时S取最大值,再根据△DFQ为直角三角形分情况求出F的坐标.
(1)将A、C两点坐标代入抛物线,得
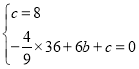 ,
,
解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8;
x+8;
(2)①∵OA=8,OC=6,
∴AC=![]() =10,
=10,
过点Q作QE⊥BC与E点,则sin∠ACB=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QE=![]() (10﹣m),
(10﹣m),
∴S=![]() CPQE=
CPQE=![]() m×
m×![]() (10﹣m)=﹣
(10﹣m)=﹣![]() m2+3m;
m2+3m;
②∵S=﹣![]() m2+3m=﹣
m2+3m=﹣![]() (m﹣5)2+
(m﹣5)2+![]() ,
,
∴当m=5时,S取最大值;
在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8的对称轴为x=
x+8的对称轴为x=![]() ,
,
∴D的坐标为(3,8),
∵CP=AQ=5,
∴CQ=5
过Q点作QG⊥x轴,
∴sin∠ACO=![]() =
=![]()
即![]()
∴QG=4
∴CG=![]()
∴OG=CO-CG=3
∴Q(3,4),
设F(![]() ,n),
,n),
当∠FDQ=90°时,则F在直线AB上,
∴F1(![]() ,8),
,8),
当∠FQD=90°时,则F的纵坐标与Q点纵坐标相同,
∴F2(![]() ,4),
,4),
当∠DFQ=90°时,设F(![]() ,n),
,n),
则FD2+FQ2=DQ2,
即![]() +(8﹣n)2+
+(8﹣n)2+![]() +(n﹣4)2=16,
+(n﹣4)2=16,
解得:n=6±![]() ,
,
∴F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ),
),
满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
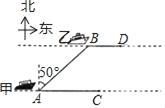
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BD于点F,交⊙O于点D,AC与BD交于点G,点E为OC的延长线上一点,且∠OEB=∠ACD.
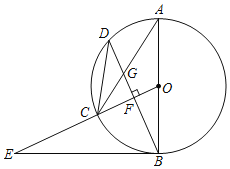
(1)求证:BE是⊙O的切线;
(2)求证:CD2=CGCA;
(3)若⊙O的半径为![]() ,BG的长为
,BG的长为![]() ,求tan∠CAB.
,求tan∠CAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
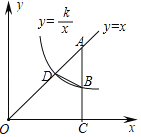
【题目】如图,直线y=x与反比例函数y=![]() (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=
(x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=![]() (x>0)的图象于点B,连接BD.
(x>0)的图象于点B,连接BD.
(1)若点B的坐标为(8,2),则k= ,点D的坐标为 ;
(2)若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
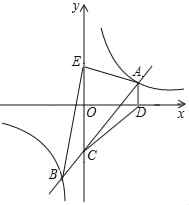
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com