
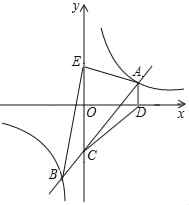
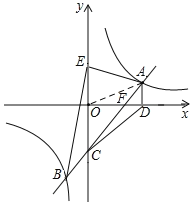
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
【答案】(1)y=x﹣4,y=![]() ;(2)32
;(2)32
【解析】
(1)依据S△AOD=S△ADC=6,可得A(6,2),将A(6,2)代入![]() ,可得到反比例函数解析式;将点A(6,2),点C(0,﹣4)代入y=kx+b,可得一次函数解析式;
,可得到反比例函数解析式;将点A(6,2),点C(0,﹣4)代入y=kx+b,可得一次函数解析式;
(2)依据E(0,4),可得CE=8,解方程组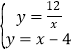 ,即可得到B(﹣2,﹣6),进而得出△ABE的面积.
,即可得到B(﹣2,﹣6),进而得出△ABE的面积.
(1)连接AO.
∵AD⊥x轴于点D,设A(a,2),∴AD=2.
∵∠CAD=45°,∴∠AFD=45°,∴FD=AD=2.
∵AD∥y轴,∴S△AOD=S△ADC=6,∴OD=6,∴A(6,2),将A(6,2)代入![]() ,得:m=12,∴反比例函数解析式为y
,得:m=12,∴反比例函数解析式为y![]() ;
;
∵∠OCF=∠CAD=45°.在△COF中,OC=OF=OD﹣FD=6﹣2=4,∴C(0,﹣4),将点A(6,2),点C(0,﹣4)代入y=kx+b,可得:
![]() ,∴
,∴![]() ,∴一次函数解析式为y=x﹣4;
,∴一次函数解析式为y=x﹣4;
(2)点E是点C关于x轴的对称点,∴E(0,4),∴CE=8,解方程组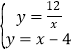 ,得:
,得:![]() 或
或![]() ,∴B(﹣2,﹣6),∴
,∴B(﹣2,﹣6),∴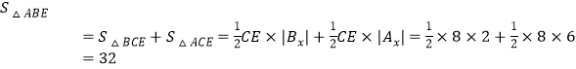 .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,对角线AC与BD交于点P,下面给出5个论断:①AB//CD;②AP=PC;③AB=CD;④∠BAD=∠DCB;⑤AD//BC.
(1)若用论断①和④作为条件,试证四边形ABCD是矩形.
(2)请你另选取两个能推出四边形ABCD为矩形的论断.如:_________和_________、___________和________________(不证明,用序号表示即可).
(3)若选取论断③和⑤作为条件,能推出四边形ABCD为矩形吗?若能,请给出证明;若不能,请举反例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
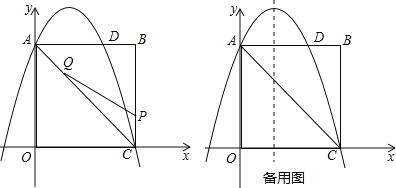
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
材料一:如果两个两位数![]() 和
和![]() 将它们各自的十位数字和个位数字交换位置后得到两个完全不同的新数
将它们各自的十位数字和个位数字交换位置后得到两个完全不同的新数![]() ,
,![]() ,这两个两位数的乘积与交换后的两个两位数的乘积相等,则称这样的两个两位数为一对“有缘数对”.
,这两个两位数的乘积与交换后的两个两位数的乘积相等,则称这样的两个两位数为一对“有缘数对”.
例如:![]() ,所以,46和96是一对“有缘数对”,
,所以,46和96是一对“有缘数对”,
材料二:在进行一些数学式计算时,我们可以把某一单项式或多项式看作一个整体,运用整体换元,使得运算更简单.
例如:计算![]() ,令:
,令:![]() ,
,
原式![]()
![]()
解决如下问题:
(1)①请任写一对“有缘数对”____________和____________.
②并探究“有缘数对”![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之间满足怎样的等量关系.并写出证明过程.
之间满足怎样的等量关系.并写出证明过程.
(2)若两个两位数![]() 与
与![]() 是一对“有缘数对,请求出这两个两位数.
是一对“有缘数对,请求出这两个两位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初三学生的中考体育备考情况,西安铁一中分校体育组从初三年级全年级学生中随机抽取部分学生进行测试,现将从报排球项目所有女生中随机抽取到的60名女生的排球成绩(40秒内有效垫球个数)进行整理,得到下列图表中信息:
垫球个数 | 频数 |
|
|
| 4 |
|
|
| 26 |
| 10 |

请根据所给信息,解答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)这60名学生垫球个数的中位数落在__________段;
(3)全校报考排球项目女生共有450人,根据以往的经验垫球个数在30个以上(包含30个)在中考中能取得良好以上成绩,请估计中考体育考试中女生排球项目达到良好以上的女生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了加强和改进学校体育工作,切实提高学生体质健康水平,决定开展“阳光体育”活动,现对全校学生感兴趣的球类项目(![]() 表示足球,
表示足球,![]() 表示篮球,
表示篮球,![]() 表示排球,
表示排球,![]() 表示羽毛球,
表示羽毛球,![]() 表示乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,张老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(部分信息未给出).
表示乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,张老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(部分信息未给出).
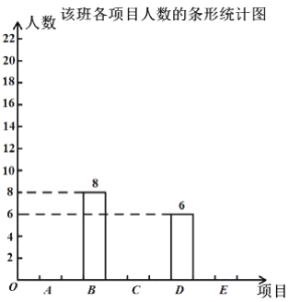
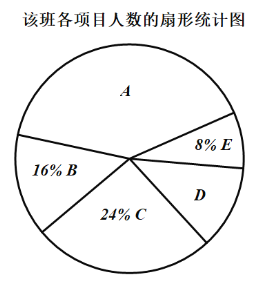
(1)求该班级学生的总人数;
(2)将条形统计图补充完整;
(3)若该校共有学生1500名,请估计有多少人选修足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com