
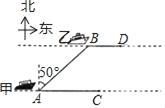
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
【答案】(1)两条航线间的距离为6.43(n mile);(2)还需要0.52h才能使两船的距离最短
【解析】
(1)过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,解直角三角形即可解决问题;
,解直角三角形即可解决问题;
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过![]() 作
作![]() 于
于![]() ,设还需要
,设还需要![]() 小时才能使两船的距离最短,构建方程即可解决问题.
小时才能使两船的距离最短,构建方程即可解决问题.
(1)过点A作AE⊥DB,交DB的延长线于E,
在Rt△AEB中,∵∠AEB=90°,∠EAB=50°,AB=10,
∴AE=ABcos50°=10×0.643=6.43(n mile),
答:两条航线间的距离为6.43(n mile);
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过C作CF⊥BD于F.
∵BE=ABsin50°=7.66,
AC=24×![]() =8,BD=15×
=8,BD=15×![]() =5,
=5,
∴DF=BD+BE﹣AC=4.66,
设还需要t小时才能使两船的距离最短,
则有:24t﹣15t=4.66,
解得t=0.52(h),
答:还需要0.52h才能使两船的距离最短.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.
(1)已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?
(2)如果在距台风中心50km的圆形区域内都将受到台风影响,那么A市受到台风影响的时间是多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月18日﹣4月20日,第29届重庆市青少年科技创新大赛在重庆南开中学举行,该校学生会在赛后对某年级各班的志愿者人数进行了统计,各班志愿者人数有6名、5名、4名、3名、2名、1名共计六种情况,并制成两幅不完整的统计图如下:
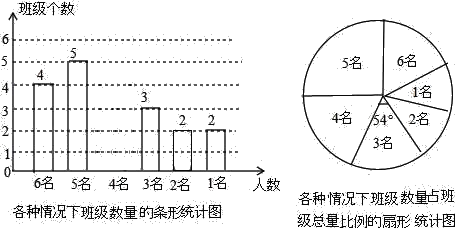
(1)该年级共有 个班级,并将条形图补充完整;
(2)求平均每班有多少名志愿者;
(3)为了了解志愿者在这次活动中的感受,校学生会准备从只有2名志愿者的班级中任选两名志愿者参加座谈会,请用列表或画树状图的方法,求出所选志愿者来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,点G是⊙O上一点,AG交CD于点K,延长KD至点E,使KE=GE,分别延长EG、AB相交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC∥EF,试探究KG、KD、GE之间的关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
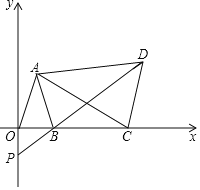
【题目】如图,在xOy中,已知点A(a﹣1,a+b),B(a,0),且![]() =0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
=0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
(1)求A、B两点坐标;
(2)求证:AO=AB;
(3)求证:∠OBP=∠OAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,还需再添加两个条件才能使
,还需再添加两个条件才能使![]() ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________.
(2)请你结合图1写出一条完美筝形的性质_______________.
(3)当图3中的∠BCD=120°时,∠AEB′=_________________.
(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称:例 筝形ABCD).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com