
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,点G是⊙O上一点,AG交CD于点K,延长KD至点E,使KE=GE,分别延长EG、AB相交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC∥EF,试探究KG、KD、GE之间的关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;
(2)连接GD,由平行线的性质得到相等的角,进而根据相似三角形的判定得到△GKD∽△EKG,然后根据相似三角形的对应边成比例可得证;
(3)连接OG,OC,根据平行线的性质得到∠E=∠ACH,然后根据已知的sinE=![]() 设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3
设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
证明:(1)如图1,连接OG.
∵KE=EG,
∴∠EKG=∠EGK,
∵∠AKH=∠EKG,
∴∠EGK=∠AKH,
∴OA=OG,
∴∠OGA=∠OAK,
∵AB⊥CD,
∴∠AHK=90°,
∴∠AKH+∠OAG=90°,
∴∠OGA+∠EGK=90°,
∴∠OGE=90°,
∴EF是⊙O的切线;
(2)KG2=KDGE,理由是:
连接GD,如图2,
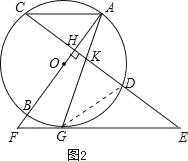
∵AC∥EF,
∴∠C=∠E,
∵∠C=∠AGD,
∴∠E=∠AGD,
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴![]() ,
,
∴KG2=KDEK,
由(1)得:EK=GE,
∴KG2=KDGE;
(3)连接OG,OC,如图3所示,
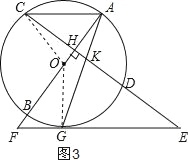
∵AC∥EF,
∴∠E=∠ACH,
∵sinE=sin∠ACH=![]() ,
,
设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=±
)2,解得t=±![]() .
.
∴CH=4![]() ,AH=3
,AH=3![]() ,
,
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,
,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3![]() )2+(4
)2+(4![]() )2=r2,解得r=
)2=r2,解得r=![]() ,
,
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() =
=![]() =
=![]() ,
,
∴FG=![]() =
=![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】已知点A(1,3)、B(3,-1),利用图中的“格点”完成下列作图并解答:

(1)在第三象限内找“格点”C,使得CA=CB,则点C的坐标是 ;
(2)在(1)的基础上,标出“格点”D,使得△DCB≌△ABC,则点D的坐标是 ;
(3)点M是x轴上一点,且MA-MB的值最大,则点M的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD与BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求∠BPD的度数;
(3)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.

(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的4月23日被联合国教科文组织确定为“世界读书日”.为满足同学们的读书需某校图书室在今年“世界读书日”期间准备到书店购买文学名著和科普读物两类图书.已知20本文学名著和40本科普读物共需1520元,20本文学名著比20本科普读物多440元(注:所采购的文学名著价格都一样,所购买的科普读物的价格都一样).
(1)每本文学名著和科普读物各多少元?
(2)若学校要求购买科普读物比文学名著多20本,科普读物和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
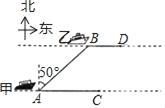
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
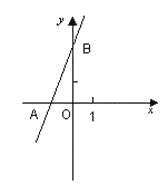
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,![]() .
.
求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com