
【题目】如图,△ABC为等边三角形,AE=CD,AD与BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求∠BPD的度数;
(3)求AD的长.

【答案】(1)详见解析;(2)60°;(3)7.
【解析】
(1)根据SAS证明△ABE与△CAD全等即可;
(2)根据全等三角形的性质得出∠ABE=∠CAD,进而解答即可;
(3)根据含30°的直角三角形的性质解答即可.
(1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠C=60°,
又∵AE=CD,
在△ABE与△CAD中, 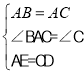 ,
,
∴△ABE≌△CAD(SAS),
∴BE=AD;
(2)解:由(1)得∠ABE=∠CAD AD=BE,
∴∠BPQ=∠BAD+∠ABE
=∠BAD+∠CAD
=60°;
(3)解:∵BQ⊥AD,∠BPQ=60°,
∴∠PBQ=30°,
∴BP=2PQ=6,
又∵AD=BE,
∴AD=BE=BP+PE=6+1=7.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=![]() (x>0)的图象经过点D.
(x>0)的图象经过点D.
(1)求点D的坐标及反比例函数的解析式;
(2)经过点C的一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于P点,当k>0时,确定点P横坐标的取值范围(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴的交点坐标分别为A(1,0),B(x2,0)(点B在点A的右侧),其对称轴是x=3,该函数有最小值是﹣2.
(1)求二次函数解析式;
(2)在图1上作平行于x轴的直线,交抛物线于C(x3,y3),D(x4,y4),求x3+x4的值;
(3)将(1)中函数的部分图象(x>x2)向下翻折与原图象未翻折的部分组成图象“G”,如图2,在(2)中平行于x轴的直线取点E(x5,y5)、(x4<x5),结合函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AE上一动点(不与点A,点E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下四个结论,①AD=BE;②CP=CQ;③OB=DE;④PQ∥AE,一定成立的结论有_____(请把正确结论的序号填在横线上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.
(1)已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?
(2)如果在距台风中心50km的圆形区域内都将受到台风影响,那么A市受到台风影响的时间是多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,点G是⊙O上一点,AG交CD于点K,延长KD至点E,使KE=GE,分别延长EG、AB相交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC∥EF,试探究KG、KD、GE之间的关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com