
【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
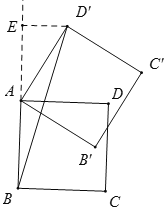
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

【答案】(1)AC垂直平分BD(2)四边形FMAN是矩形(3)BD′的平方为16+8![]() 或16–8
或16–8![]()
【解析】试题分析:(1)根据AB=AD、CB=CD可知点A、C在线段BD的垂直平分线上,从而可得;
(2)连接AF,判断出DF是AB的垂直平分线,从而可得∠FMA=90![]() ,同理可得∠FNA=90
,同理可得∠FNA=90![]() ,再根据∠MAN=90
,再根据∠MAN=90![]() ,即可判断出四边形FMAN为矩形;
,即可判断出四边形FMAN为矩形;
(3)分逆时针旋转与顺时针旋转两种情况分别讨论即可得.
试题解析:(1)∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∵点A、点C是不同的点,
∴AC⊥BD,
故答案为:垂直;
(2)猜想:四边形FMAN是矩形,理由如下:
连接AF,在Rt△ABC中,∵点F为BC的中点,
![]() AF=BF,
AF=BF,
在等腰三角形ADB中,AD=BD,
![]() FD垂直平分AB,
FD垂直平分AB,![]() ∠FMA=90
∠FMA=90![]() ,
,
同理可得∠FNA=90![]() ,又∵∠MAN=90
,又∵∠MAN=90![]() ,
,
![]() 四边形FMAN为矩形;
四边形FMAN为矩形;
(3)当逆时针旋转60度时,如图,过点D′作D′⊥AB,交BA延长线于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8+4
)2+12=8+4![]() ;
;
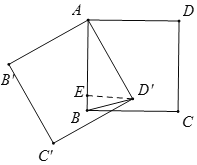
当顺时针旋转60度时,如图,过点D′作D′⊥AB,交BA于点E,
则有∠D′AE=30°,∴D′E=![]() AD′=1,AE=
AD′=1,AE=![]() ,
,
∴BE=![]() ,∴BD′2=BE2+ED′2=(
,∴BD′2=BE2+ED′2=(![]() )2+12=8-4
)2+12=8-4![]() ,
,
综上,BD′2的值为8+4![]() 或8-4
或8-4![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
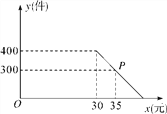
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知式子 ![]() 是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b.
是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b.

(1)则a=____,b=____.A、B两点之间的距离:____;
(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2019次时,求点P所对应的有理数.
(3)在(2)的条件下,点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距零离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知从甲地到乙地,某船顺水航行需2小时,逆水航行需3小时,
(1)设轮船在静水中前进的速度是![]() 千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
(2)如果轮船在静水中前进的速度是60千米/时,则水流的速度是多少千米/时?
查看答案和解析>>
科目:初中数学 来源: 题型:
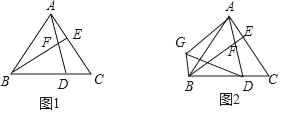
【题目】如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.
(1)求证:∠ABE=∠CAD;
(2)如图2,以AD为边向左作等边△ADG,连接BG.
ⅰ)试判断四边形AGBE的形状,并说明理由;
ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(或化简)下列各题
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8)
|×(﹣8)
(3)(﹣36)×(![]() )
)
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]()
(5)2(m﹣1)﹣(2m﹣3)
(6)(5ab+3a2)﹣2(a2+2ab)
(7)先化简,再求值:![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y),其中x=﹣2,y=
y),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C 在数轴上相距 28 个长度单位,动点 P 从点 A 出发, 以 2 单位/秒的速度沿着“折线数轴”的正方向运动,从点 O 运动到点 B 期间速度变为原来的一半; 点 P 从点 A 出发的同时,点 Q 从点 C 出发,以 1 单位秒的速度沿着“折线数轴”的负方向运动,当 点 P 到达 B 点时,点 P、Q 均停止运动. 设运动的时间为 t 秒. 问:
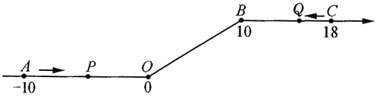
(1)当 t=3s 时,点 P 和点 O 在数轴上相距 个长度单位; 当 t=7.5s 时,点 P 和点 O 在数轴上相距 个长度单位; 当 t=9s 时,点 P 和点 Q 在数轴上相距 个长度单位.
(2)当 P、Q 两点相遇时,求出相遇时间及相遇点 M 所对应的数是多少?
(3)是否存在某一时刻使得 P、O 两点在数轴上相距的长度与 Q、B 两点在数轴上相距的长度相等? 若存在,请直接写出 t 的取值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com