
【题目】今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.
(1)已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?
(2)如果在距台风中心50km的圆形区域内都将受到台风影响,那么A市受到台风影响的时间是多长?

【答案】(1) 台风中心从B点移到D点需要6小时.(2) A市受台风影响的时间为3.75小时.
【解析】
(1)在Rt△ABD中,利用勾股定理求出BD,再根据台风的速度即可求出时间;
(2)假设A市从P点开始受到台风的影响,到Q点结束,根据题意画出图形,可知,△ADP和△ADQ全等,A市在台风从P点到Q点均受影响,即得出PQ两点的距离,便可求出A市受台风影响的时间.
解:(1)∵在Rt△ABD中,∠ADB=90°,AB=104km,AD=40km,
∴BD=![]() =96km,
=96km,
∴时间为![]() =6小时,
=6小时,
即台风中心从B点移到D点需要6小时;
(2)如图,以A为圆心,以50km为半径画弧,交BC于P、Q,则A市在P点开始受到影响,Q点恰好不受影响.
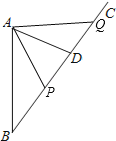
由题意,AP=AQ=50km,
在Rt△ADP中,AD=40km,
PD=![]() =30km,
=30km,
∵AP=AQ,∠ADB=90°,
∴DP=DQ=30km,
∴PQ=60km,
时间为![]() =3.75小时.
=3.75小时.
即A市受台风影响的时间为3.75小时.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图表示一个正比例函数与一个一次函数的图象,它们交于点A(3,4),一次函数的图象与y轴交于点B,且OA=0B

(1)求这两个函数的关系式;
(2)两直线与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD与BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求∠BPD的度数;
(3)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.

(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
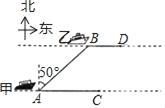
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
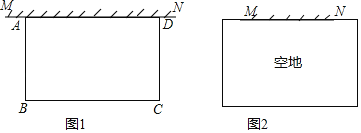
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com