
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
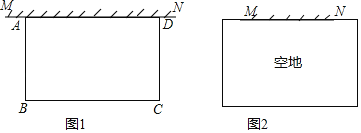
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
【答案】(1)利用旧墙AD的长为10米.(2)见解析.
【解析】
(1)按题意设出AD,表示AB构成方程;
(2)根据旧墙长度a和AD长度表示矩形菜园长和宽,注意分类讨论s与菜园边长之间的数量关系.
(1)设AD=x米,则AB=![]() 米
米
依题意得,![]() =450
=450
解得x1=10,x2=90
∵a=20,且x≤a
∴x=90舍去
∴利用旧墙AD的长为10米.
(2)设AD=x米,矩形ABCD的面积为S平方米
①如果按图一方案围成矩形菜园,依题意
得:
S=![]() ,0<x<a
,0<x<a
∵0<a<50
∴x<a<50时,S随x的增大而增大
当x=a时,S最大=50a-![]() a2
a2

②如按图2方案围成矩形菜园,依题意得
S=![]() ,a≤x<50+
,a≤x<50+![]()
当a<25+![]() <50时,即0<a<
<50时,即0<a<![]() 时,
时,
则x=25+![]() 时,S最大=(25+
时,S最大=(25+![]() )2=
)2=![]() ,
,
当25+![]() ≤a,即
≤a,即![]() ≤a<50时,S随x的增大而减小
≤a<50时,S随x的增大而减小
∴x=a时,S最大=![]() =
=![]() ,
,
综合①②,当0<a<![]() 时,
时,![]() -(
-(![]() )=
)=![]() >0
>0
![]() >
>![]() ,此时,按图2方案围成矩形菜园面积最大,最大面积为
,此时,按图2方案围成矩形菜园面积最大,最大面积为![]() 平方米
平方米
当![]() ≤a<50时,两种方案围成的矩形菜园面积最大值相等.
≤a<50时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<![]() 时,围成长和宽均为(25+
时,围成长和宽均为(25+![]() )米的矩形菜园面积最大,最大面积为
)米的矩形菜园面积最大,最大面积为![]() 平方米;
平方米;
当![]() ≤a<50时,围成长为a米,宽为(50-
≤a<50时,围成长为a米,宽为(50-![]() )米的矩形菜园面积最大,最大面积为(
)米的矩形菜园面积最大,最大面积为(![]() )平方米.
)平方米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.
(1)已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?
(2)如果在距台风中心50km的圆形区域内都将受到台风影响,那么A市受到台风影响的时间是多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,还需再添加两个条件才能使
,还需再添加两个条件才能使![]() ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE,CN、BE交于点P. 求证:∠ANC = ∠ABE.
应用:Q是线段BC的中点,连结PQ. 若BC = 6,则PQ = ___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(9,0),(0,3),OD=5,点P在BC(不与点B、C重合)上运动,当△OPD为等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________.
(2)请你结合图1写出一条完美筝形的性质_______________.
(3)当图3中的∠BCD=120°时,∠AEB′=_________________.
(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称:例 筝形ABCD).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.

(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com