
【题目】如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.

简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__________________.
(2)请你结合图1写出一条完美筝形的性质_______________.
(3)当图3中的∠BCD=120°时,∠AEB′=_________________.
(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有__________________________(写出筝形的名称:例 筝形ABCD).
【答案】正方形 答案不唯一,关于角、边、对角线、对称性等均可 80° 筝形ABCD、筝形AEOF、筝形EBCB’、筝形FDCD’、筝形OD’CB’.五个筝形
【解析】
(1)根据“完美筝形”的定义判断即可得到结果;
(2)根据题意及图形即可得出完美筝形的性质;
(3)先证出∠AEB′=∠BCB′,再求出∠BCE=∠ECF=40°,即可得出结果;
(4)由折叠的性质结合“完美筝形”的定义可得出四边形EBCB′、四边形FDCD′是“完美筝形”;由菱形的性质得出AE=AF,CE=CF,再证明△OED′≌△OFB′,得出OD′=OB′,OE=OF,证出∠AEB′=∠AFD′=90°,即可得出四边形CD′OB′、四边形AEOF是“完美筝形”;即可得出结论
解:(1)∵四边形ABCD是正方形,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴正方形是完美筝形;
(2)由完美筝形的定义可得完美筝形的边的性质是:完美筝形的两组邻边分别相等,
完美筝形的角的性质是:只有一组对角相等;

连接完美筝形的两条对角线,探究发现完美筝形的对角线的性质:完美筝形的两条对角线互相垂直;完美筝形的一条对角线平分一组对角;
完美筝形的对称性:完美筝形是轴对称图形;
证明:连接AC、BD,
∵四边形ABCD是“完美筝形”,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴△ABC≌△ADC(SAS),(完美筝形是轴对称图形)
∴∠BAC=∠DAC,∠BCA=∠DCA,(完美筝形的一条对角线平分一组对角)
∵AB=AD,∠BAC=∠DAC,
∴AC⊥BD;(完美筝形的两条对角线互相垂直)
(3)根据题意得:∠EB′C=∠B=90°,
∴在四边形CBEB′中,∠BEB′+∠BCB′=180°,
∵∠AEB′+∠BEB′=180°,
∴∠AEB′=∠BCB′,
∵∠BCE=∠ECF=∠FCD,∠BCD=120°,
∴∠BCE=∠ECF=40°,
∴∠AEB′=∠BCB′=40°+40°=80°;
(4)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有5个:筝形ABCD、筝形AEOF、筝形EBCB’、筝形FDCD’、筝形OD’CB’.:理由如下;
根据题意得:BE=B′E,BC=B′C,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,
∴四边形EBCB′、四边形FDCD′是“完美筝形”;
∵四边形ABCD是“完美筝形”,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴CD′=CB′,∠CD′O=∠CB′O=90°,
∴∠OD′E=∠OB′F=90°,
∵四边形AECF为菱形,
∴AE=AF,CE=CF,AE∥CF,AF∥CE,
∴D′E=B′F,∠AEB′=∠CB′E=90°,∠AFD′=∠CD′F=90°,
在△OED′和△OFB′中,
 ,
,
∴△OED′≌△OFB′(AAS),
∴OD′=OB′,OE=OF,
∴四边形CD′OB′、四边形AEOF是“完美筝形”;
∴包含四边形ABCD,对应图③中的“完美筝形”有5个:筝形ABCD、筝形AEOF、筝形EBCB’、筝形FDCD’、筝形OD’CB’.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
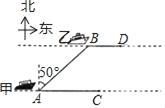
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
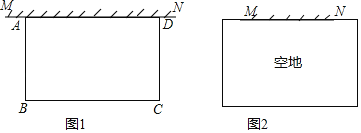
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.

(1)如图1,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标;
(2)如图2,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G⊥C′O交E′F于T点,交OC′于G点,T坐标为(3,m),求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,![]() .
.
求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象进行以下探究:
⑴请问甲乙两地的路程为 ;
⑵求慢车和快车的速度;
⑶求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图像.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com