
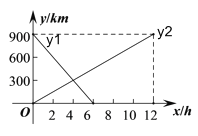
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ��������������ʻ��ʱ��Ϊx(h)������֮��ľ���Ϊy(km)��ͼ�е����߱�ʾy��x֮��ĺ�����ϵ��
����ͼ���������̽����
�����ʼ������ص�·��Ϊ ��
���������Ϳ쳵���ٶȣ�
�����߶�BC����ʾ��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�������������ʻ��ʱ��Ϊx(h),�����������ҵصľ���ֱ�Ϊy1(km)��y2(km)��������ͼ�л���y1��y2��x�ĺ���ͼ��


���𰸡���1���������ص�·��Ϊ900km��
��2���������ٶ�Ϊ![]() ���쳵���ٶ�Ϊ150km/h��
���쳵���ٶ�Ϊ150km/h��
��3���߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��4��������.
��������
��1������ͼ���ֱ�ӵó��𰸣�
��2����ͼ���֪������12h��ʻ��·��Ϊ900km����������ʻ4hʱ�������Ϳ쳵������Ȼ�������ٶȺ�·��֮��Ĺ�ϵ��⼴�ɣ�
��3���ֱ��������ó���C������Ϊ��6��450�����ѣ�4��0������6��450������y��kx��b���ô���ϵ������⣬Ȼ��д���Ա���x��ȡֵ��Χ���ɣ�
��4������쳵���������Ե���Ŀ�ĵ������ʱ�䣬���ɵó�����ͼ���ĵ�����꣬Ȼ��ͼ����.
�⣺��1����ͼ�ɵã��������ص�·��Ϊ900km��
��2����ͼ���֪������12h��ʻ��·��Ϊ900km��
�����������ٶ�Ϊ![]() ��
��
��������ʻ4hʱ�������Ϳ쳵������������ʻ��·��֮��Ϊ900km��
���������Ϳ쳵��ʻ���ٶ�֮��Ϊ![]() ��
��
���Կ쳵���ٶ�Ϊ150km/h��
��3����Ϊ�쳵��ʻ900km�����ҵأ�
���Կ쳵��ʻ![]() �����ҵأ���ʱ����֮��ľ���Ϊ
�����ҵأ���ʱ����֮��ľ���Ϊ![]() ��
��
���Ե�![]() ������Ϊ
������Ϊ![]() ��
��
���߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��![]() �����
�����![]() �����
�����![]() ��
��
�����߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��4��������ã�y1���㣨0��900����y2���㣨0��0����
�쳵���ҵص�ʱ��Ϊ��![]() ���������ص�ʱ��Ϊ��
���������ص�ʱ��Ϊ��![]() ��
��
��y1���㣨6��0����y2���㣨12��900����
��ͼ��ʾ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��,����ı���ABCD����AB=AD,CB=CD,��B=��D=90��,��ô���ǰ��������ı��ν�����������������
��һ����ͼ����ʾ��������������ֽƬABCD���۵�����ͼ����ʾ��״,��չ���õ�ͼ��,����CE,CFΪ�ۺ�,��BCE=��ECF=��FCD,��B��Ϊ��B�Ķ�Ӧ��,��D��Ϊ��D�Ķ�Ӧ��,����EB',FD���ཻ�ڵ�O��

��Ӧ�ã�
(1)��ƽ���ı��Ρ����Ρ����Ρ�����������ͼ����,һ��Ϊ����������������__________________��
(2)������ͼ1д��һ���������ε�����_______________��
(3)��ͼ3�еġ�BCD=120��ʱ,��AEB��=_________________��
(4)��ͼ2�е��ı���AECFΪ����ʱ,��Ӧͼ���е���������������__________________________(д�����ε����ƣ��� ����ABCD)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�鳤����ľ��ĸ��ⳤ��ͼ��ʾ��һֻ֩����ľ���һ������A����һֻ��Ӭ������������Ϻ�֩����ԵĶ���B����֩�뼱��ס��Ӭ�����ų�����ı�����������

(1)���D������е㣬֩������AD��DB��·�����У�����A������B�����ߵ�·��Ϊ���٣�
(2)��֩�뻹��ǰ��������������棬����Ϊ��AD-DB"�����·����������ǣ���������·�̣�����ǣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��x�ᡢy��ֱ��ڵ�A��B����OA��OB�ij���OA��OB���Ƿ���x2-10x+24=0����������P��m��n���ǵ�һ������ֱ��y=kx+b�ϵ�һ�����㣨��P�����A��B�غϣ���

(1)��ֱ��AB�Ľ���ʽ��
(2)C��x����һ�㣬��OC=2�����ACP�����S��m֮��ĺ�����ϵʽ��
(3)��x�����Ƿ����ڵ�Q��ʹ��A��B��QΪ������������ǵ��������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��3����ֱ�� BD��x�ύ�ڵ�D����ֱ��AB��ֱ��BD���ۣ���Aǡ������y���ϵ�C�㣬��ֱ��BD��Ӧ�ĺ�����ϵʽΪ______ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2����ԲO��ֱ��AB=2����P�������A��B�غ���Ϊ��Բ��һ�㣬��ͼ����BP�۵����ֱ�õ���A��O�ĶԳƵ�A�䣬O�䣬����ABP=����

��1������=15��ʱ������A����A��C��AB����ͼ1���ж�A��C���ԲO��λ�ù�ϵ����˵��������
��2����ͼ2������= ��ʱ��BA�����ԲO����������= ��ʱ����O������![]() ����
����
��3�����߶�BO�����ԲOֻ��һ��������Bʱ�������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
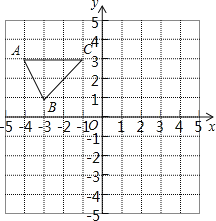
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����4��3����B����3��1����C����1��3����
��1���밴����Ҫ��ͼ��
������ABC������ƽ��4����λ���ȡ�������ƽ��2����λ���ȣ��õ���A1B1C1��������A1B1C1��
�ڡ�A2B2C2����ABC����ԭ��O�����ĶԳƣ�������A2B2C2��
��2���ڣ�1�������õ���A1B1C1����A2B2C2���ڵ�M�����ĶԳƣ���ֱ��д���Գ�����M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
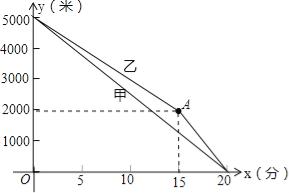
����Ŀ���ס��������˶�Ա���г���ѵ�������˾��յ��·��y���ף����ܲ�ʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ������⣺
��1�������ڽ��� �ij���ѵ������0��x��15��ʱ���ڣ��ٶȽϿ������ ��
��2������յ��·��y���ף����ܲ�ʱ��x���֣�֮��ĺ�����ϵʽ��
��3����x=15ʱ�������������ף���15��x��20��ʱ���ڣ��������ٶ�֮�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬��A=80�㣬BO��CO�ֱ�����ABC����ACB�Ľ�ƽ���ߣ�����BOC���ڣ�������

A. 140�� B. 120�� C. 130�� D. ��ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com