
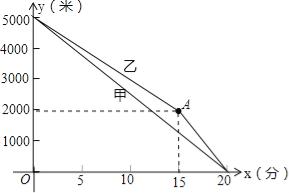
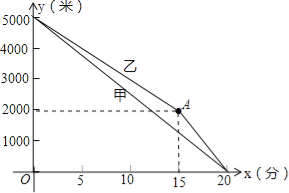
【题目】甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<x<15的时段内,速度较快的人是 ;
(2)求甲距终点的路程y(米)和跑步时间x(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
【答案】(1) 5000米,甲.(2) y=-250x+5000(0≤x≤20);(3)750米,150米/秒.
【解析】
试题根据图象信息可知,甲运动员图象经过(0,5000)(20,0)所以可用待定系数法求解.距离可根据图象求出,时间可求:20-15=5.速度=![]() 也就迎刃而解了.
也就迎刃而解了.
试题解析:(1)根据图象信息可知他们在进行5000米的长跑训练,直线倾斜程度越大表明变化大;甲.
(2)设所求直线的解析式为:y=kx+b(0≤x≤20),
由图象可知:b=5000,当x=20时,y=0,
∴0=20k+5000,解得k=-250.
即y=-250x+5000(0≤x≤20)
(3)当x=15时,y=-250x+5000=-250×15+5000=5000-3750=1250.
两人相距:(5000-1250)-(5000-2000)=750(米).
两人速度之差:![]() =150(米/分).
=150(米/分).


科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象进行以下探究:
⑴请问甲乙两地的路程为 ;
⑵求慢车和快车的速度;
⑶求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图像.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一假期,小丽到荷花湖风景区游玩,她去时全程约84千米,返回时全程约45千米.小丽所乘汽车去时的平均速度是返回时的1.2倍,所用时间却比返回时多20分钟.求小丽所乘汽车返回时的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=-x+4与x轴,y轴分别交于A,B两点,点P(m,5)为直线l上一点.动点C从原点O出发,以每秒1个单位长度的速度沿y轴正方向运动.设点C的运动时间为t秒.
(1)①m= ;
②当t= 时,△PBC的面积是1.
(2)请写出点C在运动过程中,△PBC的面积S与t之间的函数关系式;
(3)点D、E分别是直线AB、x轴上的动点,当点C运动到线段QB的中点时(如右图),△CDE周长的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
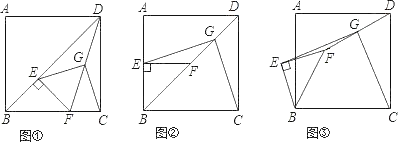
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com