
【题目】如图,直线l:y=-x+4与x轴,y轴分别交于A,B两点,点P(m,5)为直线l上一点.动点C从原点O出发,以每秒1个单位长度的速度沿y轴正方向运动.设点C的运动时间为t秒.
(1)①m= ;
②当t= 时,△PBC的面积是1.
(2)请写出点C在运动过程中,△PBC的面积S与t之间的函数关系式;
(3)点D、E分别是直线AB、x轴上的动点,当点C运动到线段QB的中点时(如右图),△CDE周长的最小值是 .

【答案】(1)1;2或6(2)见解析(3)2![]() .
.
【解析】
(1)①把点P(m,5)代入y=x+4即可求得;
②得到B的坐标,表示出BC,根据三角形面积公式得到关于t的方程,解得即可;
(2)根据三角形面积公式列出即可;
(3)作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小,依据勾股定理即可得到FG的长,进而得到△CDE周长的最小值.
(1)①∵点P(m,5)为直线l上一点,
∴5=m+4,
解得m=1,
故答案为1;
②由直线l:y=x+4可知A(4,0),B(0,4),
由题意可知:BC=4t或BC=t4,
∵S△PBC=![]() BC|xP|=1,
BC|xP|=1,
∴![]() (4t)×1=1或
(4t)×1=1或![]() (t4)×1=1,
(t4)×1=1,
解得t=2或t=6;
故答案为2或6;
(2)∵BC=4t或BC=t4,
∴△PBC的面积S与t的函数关系式为S=
(3)如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,

∵点C是OB的中点,
∴BC=CO=2,OG=2,BG=6,
易得∠ABC=45°,
∴△BCF是等腰直角三角形,
∴BF=BC=2,
由轴对称的性质,可得DF=DC,EC=EG,
当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
∵Rt△BFG中,FG=![]() ,
,
∴△CDE周长的最小值是2![]() .
.
故答案为2![]() .
.
【点晴】
本题是一次函数的综合题,考查了一次函数图象上的点的坐标特征,待定系数法求解析式,等腰三角形的性质,三角形的面积,轴对称最短路线问题,解题的关键是利用对称性在找到△CDE周长的最小时点D、点E位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.


科目:初中数学 来源: 题型:
【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.

(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
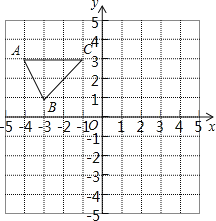
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
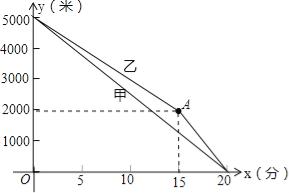
【题目】甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<x<15的时段内,速度较快的人是 ;
(2)求甲距终点的路程y(米)和跑步时间x(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
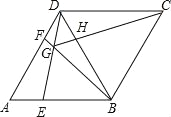
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线![]() 是
是![]() 的角平分线,
的角平分线,![]() ,点
,点![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() .
.
(1)如图1,当点![]() 在射线
在射线![]() 上时,连接
上时,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 的形状是_____.
的形状是_____.
(2)如图2,当点![]() 在射线
在射线![]() 的反向延长线
的反向延长线![]() 上时,连接
上时,连接![]() ,
,![]() .若
.若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中A(1,1),B(2,1),C(1,3),用信号枪沿直线y=3x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是( )

A.﹣5≤b≤0B.﹣5<b≤﹣3C.﹣5≤b≤3D.﹣5≤b≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )

A. 140° B. 120° C. 130° D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
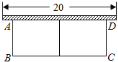
【题目】如图,有长为![]() 的篱笆,一面利用墙(墙的最大可用长度为
的篱笆,一面利用墙(墙的最大可用长度为![]() ),围成中间隔有一道篱笆(平行于
),围成中间隔有一道篱笆(平行于![]() )的矩形花圃
)的矩形花圃![]() .设花圃的一边
.设花圃的一边![]() 为
为![]() .
.
![]() 则
则![]() ________(用含
________(用含![]() 的代数式表示),矩形
的代数式表示),矩形![]() 的面积
的面积![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
![]() 如果要围成面积为
如果要围成面积为![]() 的花圃,
的花圃,![]() 的长是多少?
的长是多少?
![]() 将
将![]() 中表示矩形
中表示矩形![]() 的面积的代数式通过配方,问:当
的面积的代数式通过配方,问:当![]() 等于多少时,能够使矩形花圃
等于多少时,能够使矩形花圃![]() 面积最大,最大的面积为多少?
面积最大,最大的面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com