
【题目】如图,已知直线AB与x轴交于点A(4,0)、与y轴交于点B(0,3),直线 BD与x轴交于点D,将直线AB沿直线BD翻折,点A恰好落在y轴上的C点,则直线BD对应的函数关系式为______ .

【答案】y=-2x+3
【解析】
过点D作DE⊥AB于E,根据折叠的性质可得∠ABD=∠CBD,求出DO=DE,BO=BE=3,然后设DO=DE=x,则DA=4-x,在Rt△ADE中,利用勾股定理构造方程,求出x的长,即可得到D点坐标,然后再利用待定系数法求解析式即可.
解:过点D作DE⊥AB于E,
∵将直线AB沿直线BD翻折,点A恰好落在y轴上的C点,
∴∠ABD=∠CBD,
∵DO⊥BO,DE⊥AB,
∴DO=DE,
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=![]() ,
,
易证△OBD≌△EBD,
∴BO=BE=3,
设DO=DE=x,则DA=4-x,
在Rt△ADE中,DE2+AE2=DA2,即x2+(5-3)2=(4-x)2,
解得:![]() ,
,
∴D(![]() ,0),
,0),
设直线BD的解析式为:y=kx+b(k≠0),
代入B(0,3),D(![]() ,0),得
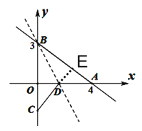
,0),得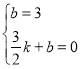 ,解得:
,解得:![]() ,
,
∴直线BD的解析式为:![]() ,
,
故答案为:![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,![]() .
.
求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
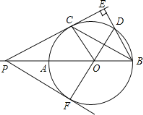
【题目】如图,![]() 是
是![]() 的直径,延长
的直径,延长![]() 至点
至点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,切点为
,切点为![]() ,过点
,过点![]() 向
向![]() 的延长线作垂线
的延长线作垂线![]() 交该延长线于点
交该延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
![]() 求
求![]() 的长;
的长;
![]() 连结
连结![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
①求![]() 的长;
的长;
②求证:![]() 是
是![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,抛物线![]() 与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,
与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,
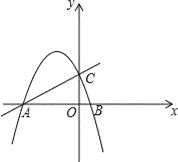
(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=2AO,求P,Q的坐标;
(3)动点M在直线y=x+4上,且△ABC与△COM相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长8千米,另一条公路BC长是6千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )
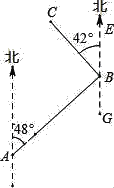
A. 6千米 B. 8千米 C. 10千米 D. 14千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象进行以下探究:
⑴请问甲乙两地的路程为 ;
⑵求慢车和快车的速度;
⑶求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图像.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一假期,小丽到荷花湖风景区游玩,她去时全程约84千米,返回时全程约45千米.小丽所乘汽车去时的平均速度是返回时的1.2倍,所用时间却比返回时多20分钟.求小丽所乘汽车返回时的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
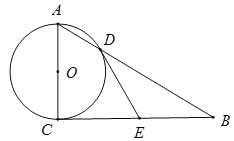
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com