
【题目】如图,![]() 是
是![]() 的直径,延长
的直径,延长![]() 至点
至点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,切点为
,切点为![]() ,过点
,过点![]() 向
向![]() 的延长线作垂线
的延长线作垂线![]() 交该延长线于点
交该延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
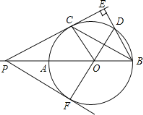
![]() 求
求![]() 的长;
的长;
![]() 连结
连结![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
①求![]() 的长;
的长;
②求证:![]() 是
是![]() 的切线.
的切线.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②见解析
;②见解析
【解析】
(1)在直角△OPC中,利用勾股定理即可得到圆的半径长,然后利用相似三角形的性质求得BE的长;
(2)①证明△OBD是等边三角形,即可求得DE的长;
②首先证明△OPC≌△OPF,根据切线的判定定理即可证得.
(1)设圆的半径是r,则OP=PA+r=1+r,OC=r,PC=![]() r.
r.
∵PC是圆的切线,∴∠PCO=90°,在直角△PCO中,PC2+OC2=OP2,即(![]() r)2+r2=(1+r)2,解得:r=1或r=﹣
r)2+r2=(1+r)2,解得:r=1或r=﹣![]() (舍去负值).
(舍去负值).
在直角△OPC中,cos∠POC=![]() =
=![]() ,∴∠POC=60°.
,∴∠POC=60°.
∵∠PCO=90°,BE⊥BC,∴BE∥OC,∴△OPC∽△BPE,∠OBD=∠POC=60°,∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() OC=
OC=![]() ;
;
(2)①在△OBD中,OB=OD,∠OBD=60°,∴△OBD是等边三角形,BD=OB=1,∠BOD=60°,∴DE=BE﹣BD=![]() ﹣1=
﹣1=![]() ;
;
②∵∠POC=60°,∠BOD=60°,∴∠POF=60°,∴∠POC=∠POF.在△OPC和△OPF中,∵ ,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.
,△OPC≌△OPF(SAS),∴∠OFP=∠OCP=90°,∴PF是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于于点P.

(1)求证:△ACE ≌ △BCD.
(2)求∠AOB的度数.
(3)连接OC,求证:OC平分∠AOD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() .
.
(1)在所给坐标系中作出![]() 关于y轴的对称图形
关于y轴的对称图形![]() ;
;
(2)分别写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,在所给坐标系中作出点
的周长最小,若存在,在所给坐标系中作出点![]() (不写作法,保留作图痕迹)并写出点
(不写作法,保留作图痕迹)并写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]()
![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图像为
的图像为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.

(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l与坐标轴相交于点M(3,0),N(0,﹣4),反比例函数y=![]() (x>0)的图象经过Rt△MON的外心A.
(x>0)的图象经过Rt△MON的外心A.

(1)求直线l的解析式;
(2)直接写出点A坐标及k值;
(3)在函数y=![]() (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△OMP的面积与△OBC的面积相等,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△OMP的面积与△OBC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与x轴交于点A(4,0)、与y轴交于点B(0,3),直线 BD与x轴交于点D,将直线AB沿直线BD翻折,点A恰好落在y轴上的C点,则直线BD对应的函数关系式为______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
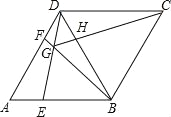
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com