
【题目】如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于于点P.

(1)求证:△ACE ≌ △BCD.
(2)求∠AOB的度数.
(3)连接OC,求证:OC平分∠AOD
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)利用等边三角形的性质证明![]() ;
;
(2)由![]() 得到∠CBD=∠CAE.再利用三角形内角和等于180°,由△APC和△BPO中有内角互为对顶角进而得出∠BOA=∠ACP=60°.
得到∠CBD=∠CAE.再利用三角形内角和等于180°,由△APC和△BPO中有内角互为对顶角进而得出∠BOA=∠ACP=60°.
(3)过C点作CG⊥AE,CH⊥BD,由三角形全等可得其对应高相等.再根据到角两边距离相等的点在角平分线即可得出结论.
(1)证明:![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
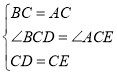 ,
,
![]() (SAS).
(SAS).
(2)![]() .
.
∴∠CBD=∠CAE,
∵∠BPO =∠APC,
又∵∠CBD+∠BPO+∠BOP=∠CAE+∠APC+∠ACP=180°.
∴∠BOP=∠ACP=60°,即∠AOB=60°.
(3)如图,过C点作CG⊥AE,CH⊥BD,
![]() ,
,
∴![]() ,AE=BD,
,AE=BD,
∴![]() ,
,
∴CG=CH,
又∵CG⊥AE,CH⊥BD,
∴OC是∠AOD的角平分线,即OC平分∠AOD.


科目:初中数学 来源: 题型:
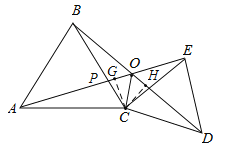
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. ![]() 一定是一次函数
一定是一次函数
B. 有的实数在数轴上找不到对应的点
C. 长为![]() 的三条线段能组成直角三角形
的三条线段能组成直角三角形
D. 无论![]() 为何值,点
为何值,点![]() 总是在第二象限
总是在第二象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,![]() .
.
求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
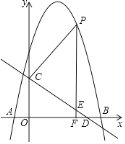
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①长度相等的弧是等弧;②平分弦的直径垂直于弦;③直径是弦;④同弧或等弧所对的圆心角相等;⑤在同圆或等圆中,相等的弦所对弧相等;错误的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,延长
的直径,延长![]() 至点
至点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,切点为
,切点为![]() ,过点
,过点![]() 向
向![]() 的延长线作垂线
的延长线作垂线![]() 交该延长线于点
交该延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
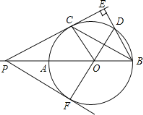
![]() 求
求![]() 的长;
的长;
![]() 连结
连结![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
①求![]() 的长;
的长;
②求证:![]() 是
是![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com