【题目】如图，在
和
中，
，还需再添加两个条件才能使
，则不能添加的一组条件是（ ）
A. AC=DE，∠C=∠EB. BD=AB，AC=DE
C. AB=DB，∠A=∠DD. ∠C=∠E，∠A=∠D
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若DE=5，BD=3，则线段CE的长为（ ）
A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
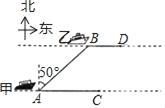
【题目】如图，海面上甲、乙两船分别从A，B两处同时出发，由西向东行驶，甲船的速度为24n mile/h，乙船的速度为15n mile/h，出发时，测得乙船在甲船北偏东50°方向，且AB=10nmile，经过20分钟后，甲、乙两船分别到达C，D两处．
（参考值：sin50°≈0.766，cos50°≈0.643，tan50°≈1.192）
（1）求两条航线间的距离；
（2）若两船保持原来的速度和航向，还需要多少时间才能使两船的距离最短？（精确到0.01）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示，顶点A、F分别在两条平行线上．若A、D、F在一条直线上，则∠1与∠2的数量关系是（ ）
A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2． D. ∠1+2∠2=90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是______．(填序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），
C（3，4）
⑴ 作出与△ABC关于y轴对称△A1B1C1，并写出 三个顶点的坐标为：A1（ ），B1（ ），C1（ ）；
⑵ 在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标；
⑶ 在 y 轴上是否存在点 Q，使得S△AOQ=
S△ABC，如果存在，求出点 Q 的坐标，如果不存在，说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
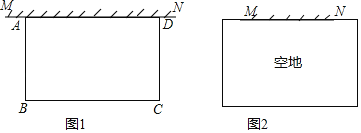
【题目】空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．
（1）已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．如图1，求所利用旧墙AD的长；
（2）已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园ABCD的面积最大，并求面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，OA＝6，OC＝10.
(1)如图1，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点，求E点的坐标；
(2)如图2，在OA、OC边上选取适当的点E′、F，将△E′OF沿E′F折叠，使O点落在AB边上的D′点，过D′作D′G⊥C′O交E′F于T点，交OC′于G点，T坐标为(3，m)，求m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
