
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )

A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中结论正确的个数有()
=AB:AC.其中结论正确的个数有()
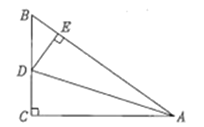
A.5个B.4个
C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月18日﹣4月20日,第29届重庆市青少年科技创新大赛在重庆南开中学举行,该校学生会在赛后对某年级各班的志愿者人数进行了统计,各班志愿者人数有6名、5名、4名、3名、2名、1名共计六种情况,并制成两幅不完整的统计图如下:
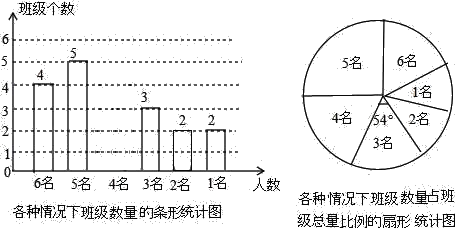
(1)该年级共有 个班级,并将条形图补充完整;
(2)求平均每班有多少名志愿者;
(3)为了了解志愿者在这次活动中的感受,校学生会准备从只有2名志愿者的班级中任选两名志愿者参加座谈会,请用列表或画树状图的方法,求出所选志愿者来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
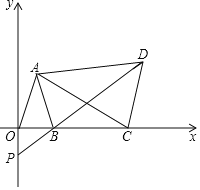
【题目】如图,在xOy中,已知点A(a﹣1,a+b),B(a,0),且![]() =0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
=0,C为x轴上B点右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y轴于点P.
(1)求A、B两点坐标;
(2)求证:AO=AB;
(3)求证:∠OBP=∠OAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
![]() 甲、乙两车单独完成任务分别需要多少天?
甲、乙两车单独完成任务分别需要多少天?
![]() 已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元
已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元![]() 试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,还需再添加两个条件才能使
,还需再添加两个条件才能使![]() ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE,CN、BE交于点P. 求证:∠ANC = ∠ABE.
应用:Q是线段BC的中点,连结PQ. 若BC = 6,则PQ = ___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com