
【题目】今年4月18日﹣4月20日,第29届重庆市青少年科技创新大赛在重庆南开中学举行,该校学生会在赛后对某年级各班的志愿者人数进行了统计,各班志愿者人数有6名、5名、4名、3名、2名、1名共计六种情况,并制成两幅不完整的统计图如下:
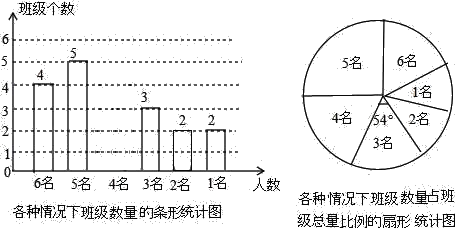
(1)该年级共有 个班级,并将条形图补充完整;
(2)求平均每班有多少名志愿者;
(3)为了了解志愿者在这次活动中的感受,校学生会准备从只有2名志愿者的班级中任选两名志愿者参加座谈会,请用列表或画树状图的方法,求出所选志愿者来自同一个班级的概率.
【答案】(1)20,补图见解析;(2)平均每班有4名志愿者;(3)![]() .
.
【解析】
(1)可以通过那个扇形图中的那个人数为三名的班级为三个所占圆心角为54度即可求出年级总的班级数,(2)根据补充完整的条形图,根据各组志愿者不同情况下班级个数就可得到全年级总的志愿者人数,然后除以班级数即可得到答案,(3)根据列表法和画树状图的方法可以计算出该概率.
(1)∵3名的圆心角为54°,
∴占![]() ×100%=15%,
×100%=15%,
∴该年级的班级数为:3÷15%=20(个),
∴4名:20﹣4﹣5﹣3﹣2﹣2=4(个).
故答案为:20;
(2)![]() =4(名),
=4(名),
答:平均每班有4名志愿者;
(3)画树状图得:
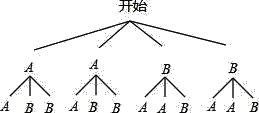
∵共有12种等可能的结果,所选志愿者来自同一个班级的4种情况,
∴所选志愿者来自同一个班级的概率为:![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数学的趣味无处不在,在学习数学的过程中,小明发现了有规律的等式:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
(1)从计算过程中找出规律,可知:
①![]() ;
;
② =![]() .
.
(2)计算:![]() (结果用含n的式子表示)
(结果用含n的式子表示)
(3)对于算式:![]()
①计算出算式的值(结果用乘方表示);
②直接写出结果的个位数字是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.

(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6.
(k>0)上一点,且在第一象限内,若△AOC的面积为6.
(1)求双曲线的解析式;
(2)求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
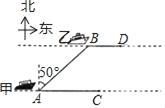
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )

A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.

(1)如图1,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标;
(2)如图2,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G⊥C′O交E′F于T点,交OC′于G点,T坐标为(3,m),求m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com