
【题目】已知二次函数y=ax2+bx+c的图象经过A(n,b),B(m,a)且m+n=1.
(1)当b=a时,直接写出函数图象的对称轴;
(2)求b和c(用只含字母a、n的代数式表示):
(3)当a<0时,函数有最大值-1,b+c≥a,n≤![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ≤a≤
≤a≤![]() .
.
【解析】
(1)用抛物线对称轴公式求解;
(2)将A(n,b),B(m,a)代入解析式,用待定系数法求解;
(3)由b+c的值列不等式求得n的取值范围,然后将二次函数配方为顶点式后根据题意可得![]() ,然后将b和c代入化简求得
,然后将b和c代入化简求得![]() ,然后根据n的取值范围求得a的取值范围.
,然后根据n的取值范围求得a的取值范围.
解:(1)由题意可得
抛物线的对称轴为:直线![]()
(2)因为二次函数![]() 经过A(n,b),B(m,a),
经过A(n,b),B(m,a),
所以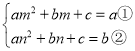
方程组①-②,得
![]() ,
,
![]() ,
,
∵m-n=1, a![]() ,
,
∴![]() ,
,
得![]() ,
,
把![]() 代入方程组中②,得
代入方程组中②,得
![]() ,
,
(3)由(2)可知:![]()
又![]()
![]() ≥a
≥a
![]()
![]() ≥a,
≥a,
当a<0时,n≥![]() ,
,
由n≤![]() 得,
得,![]() ≤n≤
≤n≤![]() ,
,
∵![]() ,a<0
,a<0
![]()
![]()
![]()
![]() ,且
,且![]() ,得
,得
![]() ,
,
化简得,![]() ,
,
∴![]() ,
,
配方得![]() ,
,
∵![]() 在
在![]() ≤n≤
≤n≤![]() 时随n的增大而增大
时随n的增大而增大
![]() 当n=
当n=![]() 时,
时,![]() ,当n=
,当n=![]() 时,
时,![]()
![]()
![]()
![]() ≤a≤
≤a≤![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于圆,点D在劣弧![]() 上,AD=
上,AD=![]() BC,DC=
BC,DC=![]() AB,Q为AC中点,点D与点P关于点Q对称.
AB,Q为AC中点,点D与点P关于点Q对称.
(1)求证:△PAD∽△ABC.
(2)求证:点B,P,D在一条直线上.
(3)如图2,记∠PAB=α,∠PCB=β,∠ABC=θ,请用含α,β的代数式表示θ.
(4)如图3,设E,F分别为AB,BC的中点,EF交BD于点H,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
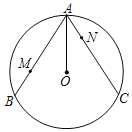
【题目】如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
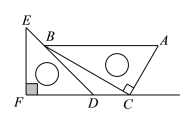
【题目】将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,∠F=∠ACB=90°,AB∥CF,∠E=45°,∠A=60°,AC=8,则CD的长度是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
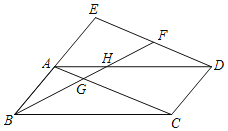
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使得AE=AB,联结DE、AC.点F在线段DE上,联结BF,分别交AC、AD于点G、H.
(1)求证:BG=GF;
(2)如果AC=2AB,点F是DE的中点,求证:AH2=GHBH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
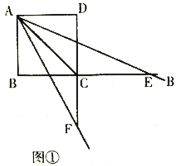
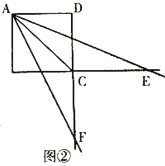
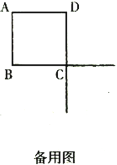
【题目】已知正方形ABCD的边长为8,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图①,当a=8时,b的值为 ;
(2)如图②,当∠EAF被对角线AC平分时,求a、b的值;
(3)请写出∠EAF绕点A旋转的过程中a,b满足的关系式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com