
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,又因为BF=AC所以CE=
AC,又因为BF=AC所以CE=![]() AC=
AC=![]() BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
解:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.故①正确;
在Rt△DFB和Rt△DAC中,
∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
又∵∠BDF=∠CDA=90°,BD=CD,
∴△DFB≌△DAC.
∴BF=AC;DF=AD.
∵CD=CF+DF,
∴AD+CF=BD;故②正确;
在Rt△BEA和Rt△BEC中
∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵BE=BE,∠BEA=∠BEC=90°,
∴Rt△BEA≌Rt△BEC.
∴CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
∴CE=![]() AC=
AC=![]() BF;故③正确;
BF;故③正确;
连接CG.
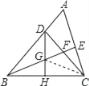
∵△BCD是等腰直角三角形,
∴BD=CD
又DH⊥BC,
∴DH垂直平分BC.
∴BG=CG
在Rt△CEG中,
∵CG是斜边,CE是直角边,
∴CE<CG.
∵CE=AE,
∴AE<BG.故④错误.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?
(4)直角坐标系中的横轴和纵轴上的单位长度取得不一致,这对问题的结论有影响吗?允许这样做吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴.
(1)试判断点A(-1,a)是否是直线l的“伴侣点”?请说明理由;
(2)若点P(2m-5,8)是直线l的“伴侣点”,求m的取值范围;
(3)若点A(-1,a)、B(b,2a)、C(-![]() ,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为
,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为![]() ,试判断点B是否是直线l的“伴侣点”?请说明理由.
,试判断点B是否是直线l的“伴侣点”?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.

(1)求证:DC//AB.
(2)求∠AFE的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
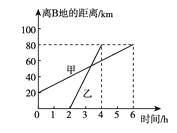
【题目】如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题:
(1)A,B两地哪个距C地近?近多少?
(2)甲、乙两人谁出发时间早?早多长时间?
(3)甲、乙两人在途中行驶的平均速度分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用二元一次方程组解决问题:近日由于城市地下水管老旧破裂,全市停水.小明去超市购买生活用水,已知大桶矿泉水每桶5升,价值10.5元,小瓶矿泉水每瓶500毫升,价值1.5元.(1升=1000毫升)
(1)若小明要购买1大桶矿泉水和3小瓶矿泉水,需要 元;
(2)若小明生活用水总量为20升,共花费46.5元,问这两种矿泉水各买多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工地有72m2的墙面需要粉刷.若安排4名一级技工粉刷一天,结果还剩12m2墙面未能刷完;同样时间内安排6名二级技工去粉刷,则刚好全部刷完.己知每名一级技工比二级技工一天多粉刷3m2墙面.设每一名一级技工一天粉刷墙面xm2.
(1)每名二级技工一天粉刷墙面_____m2(用含x的式子表示);
(2)求每名一级技工、二级技工一天分别能粉刷多少m2墙面?
(3)每名一级技工一天的施工费是300元,每名二级技工一天的施工费是200元.若另一工地有540m2的墙面需要粉刷,要求一天完工且施工总费用不超过10600元,则至少需要_____名二级技工(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com