
【题目】如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题:
(1)A,B两地哪个距C地近?近多少?
(2)甲、乙两人谁出发时间早?早多长时间?
(3)甲、乙两人在途中行驶的平均速度分别为多少?
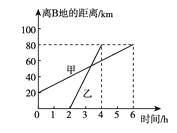
【答案】(1)A地距C地近,近20km;(2)甲出发时间早,早2h;(3)甲的平均速度为10km/h,乙的平均速度为40km/h.
【解析】
(1)根据图象中,刚开始时,甲从A地出发,离B地的距离为![]() ,随着时间的增大,离B地的距离越远,从而可知A地在B、C两地的中间,由此即可得出答案;
,随着时间的增大,离B地的距离越远,从而可知A地在B、C两地的中间,由此即可得出答案;
(2)由乙的图象可知,前![]() ,乙离B地的距离为
,乙离B地的距离为![]() ,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,由此即可得出答案;
,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,由此即可得出答案;
(3)根据“速度![]() 路程
路程![]() 时间”即可得.
时间”即可得.
(1)由图象可知,刚开始时,甲从A地出发,离B地的距离为![]() ,随着时间的增大,离B地的距离越远
,随着时间的增大,离B地的距离越远
则A地在B、C两地的中间
故A地距C地近,近![]() ;
;
(2)由乙的图象可知,前![]() ,乙离B地的距离为
,乙离B地的距离为![]() ,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,说明甲已出发
,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,说明甲已出发
故甲出发时间早,早![]() ;
;
(3)甲的平均速度为![]()
乙的平均速度为![]()
答:甲的平均速度为![]() ,乙的平均速度为
,乙的平均速度为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C,D,B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)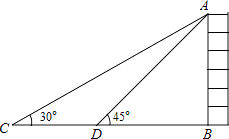
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ACB=62°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.

求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90°( )
∴EF∥AD( )
∴∠1=∠BAD( )
又∵∠1=∠2(已知)
∴ (等量代换)
∴DG∥BA.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小新家、小华家和书店依次在东风大街同一侧(忽略三者与东风大街的距离).小新小华两人同时各自从家出发沿东风大街匀速步行到书店买书,已知小新到达书店用了20分钟,小华的步行速度是40米/分,设小新、小华离小华家的距离分别为y1(米)、y2(米),两人离家后步行的时间为x(分),y1与x的函数图象如图所示,根据图象解决下列问题:
(1)小新的速度为_____米/分,a=_____;并在图中画出y2与x的函数图象
(2)求小新路过小华家后,y1与x之间的函数关系式.
(3)直接写出两人离小华家的距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(习题回顾)(1)如下左图,在![]() 中,
中,![]() 平分
平分![]() 平分
平分![]() ,则
,则![]() _________
_________![]() .
.

(探究延伸)在![]() 中,
中,![]() 平分
平分![]() 、
、![]() 平分
平分![]() 、
、![]() 平分
平分![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(2)如上中间图,求证:![]() ;
;
(3)如上右图,![]() 外角
外角![]() 的平分线
的平分线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
①判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
②若![]() ,试说明:
,试说明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com