
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ACB=62°,求∠BDC的度数.

科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ相交于O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.

(1)如图1,∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线,试求出∠AEB的度数.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)在(2)的条件下,在△CDE中,如果有一个角是另一个角的2倍,请直接写出∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:
单价/万元 | 工作效率/(只/h) | |
A种型号 | 16 | 4000 |
B种型号 | 14.8 | 3000 |
(1)求购进A,B两种型号的口罩生产线各多少台.
(2)现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴.
(1)试判断点A(-1,a)是否是直线l的“伴侣点”?请说明理由;
(2)若点P(2m-5,8)是直线l的“伴侣点”,求m的取值范围;
(3)若点A(-1,a)、B(b,2a)、C(-![]() ,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为
,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为![]() ,试判断点B是否是直线l的“伴侣点”?请说明理由.
,试判断点B是否是直线l的“伴侣点”?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
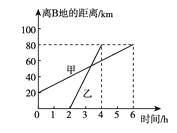
【题目】如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题:
(1)A,B两地哪个距C地近?近多少?
(2)甲、乙两人谁出发时间早?早多长时间?
(3)甲、乙两人在途中行驶的平均速度分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丹、小林是某中学八年级的同班同学,在升入九年级时,学校打算重新组班,他们将被随机编入A,B,C三个班.
(1)请你用画树状图法或列表法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com