
����Ŀ���¹ڷ��������ڼ䣬ij���ֳ�Ϊ��������Ŀ������������������������456��Ԫ����A��B�����ͺŵĿ��ֻ���30̨�������ͺſ��ֻ��ĵ��ۺ���Ч�ʷֱ����±���
����/��Ԫ | ����Ч��/��ֻ/h�� | |
A���ͺ� | 16 | 4000 |
B���ͺ� | 14.8 | 3000 |
��1����A��B�����ͺŵĿ��������߸�����̨��
��2������200��ֻ���ֵ��������ƻ������¹����Ŀ��ֻ���15̨ͬʱ�����������������Ĺ���ÿ�칤��8h������������A���ͺŵĿ��ֻ�����̨������5�����������
���𰸡���1������A��B�����ͺŵĿ��������߷ֱ�Ϊ10̨��20̨����2����������A���ͺŵĿ��ֻ�5̨������5�����������
��������
��1���蹺��![]() ���ͺŵ�������Ϊ
���ͺŵ�������Ϊ![]() ̨����
̨����![]() ���ͺŵ�������Ϊ
���ͺŵ�������Ϊ![]() ̨���з��̿ɵô𰸣�
̨���з��̿ɵô𰸣�
��2������������A���ͺŵĿ��ֻ�![]() ̨������5��������������ⲻ�ȹ�ϵ���в���ʽ�ɵô𰸣�
̨������5��������������ⲻ�ȹ�ϵ���в���ʽ�ɵô𰸣�
�⣺��1���蹺��![]() ���ͺŵ�������Ϊ
���ͺŵ�������Ϊ![]() ̨����
̨����![]() ���ͺŵ�������Ϊ
���ͺŵ�������Ϊ![]() ̨��
̨��
��![]()
��ã�![]() ��
��
���ԣ�![]()
������A��B�����ͺŵĿ��������߷ֱ�Ϊ10̨��20̨��
��2������������A���ͺŵĿ��ֻ�![]() ̨������5�������������
̨������5�������������
![]()
![]()
��ã�![]()
��������A���ͺŵĿ��ֻ�5̨������5�����������


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�����ڵ̱�A���������ӵ�AC��ˮƽ��ļн�Ϊ30�㣬AC�ij�Ϊ ![]() �ף�����AO��ˮƽ�ߵļн�Ϊ60�㣬�䳤Ϊ3�ף���AO�������OB�ļн�Ϊ60�㣬��ƯB��ӵ��¶�C֮��ľ��룮
�ף�����AO��ˮƽ�ߵļн�Ϊ60�㣬�䳤Ϊ3�ף���AO�������OB�ļн�Ϊ60�㣬��ƯB��ӵ��¶�C֮��ľ��룮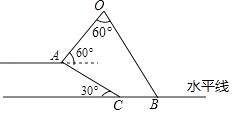
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ��ѧ��ȤС��Ϊ��ô���AB�ĸ߶ȣ��ڴ���ǰ��ƽ����ѡ��һ��C����ô��ö���A������Ϊ30�㣬������÷���ǰ��80�ף������D����C��D��B������ͬһֱ���ϣ����ֲ�ô��ö���A������Ϊ45�㣬�������ô��õĸ߶ȣ�����ȷ��0.1�ף��ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��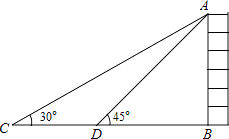
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��a��0������B��2��a��0������A��B����ߣ���C��1����1��������AC��BC������AB��BC��AC��Χ�������ڣ����߽磩��������������궼Ϊ�����ĵ�ĸ���Ϊ4������ôa��ȡֵ��ΧΪ������
A. ��1��a��0B. 0��a��1C. ��1��a��1D. ��2��a��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У��е�P��a��b����ʵ��a��b��m��������������ʽ��
2a��3m+1=0��3b��2m��16=0
��1����a=1ʱ����P��x��ľ���Ϊ�� ����
��2������P����x���ϣ���Pƽ�ƺ��Ӧ��ΪP����a+15��b+4�������P��P�������ꣻ
��3����a��4��bʱ����m����С����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��C��B����ͬһ��ֱ���ϣ�AD��BE��
��1����ͼ�٣�����A=48������B=128��ʱ�����C�Ķ�����
��2����ͼ�ڣ�AQ��BQ�ֱ�Ϊ��DAC����EBC��ƽ��������ֱ�ߣ���̽����C���AQB��������ϵ��
��3����ͼ�ۣ��ڣ�2����ǰ���£�����AC��QB��QP��PB��ֱ��д����DAC����ACB����CBE��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У��Խ���AC��BD���ڵ�O��AB=AC����E��BD��һ�㣬��AE=AD����EAD=��BAC��
��1����֤����ABD=��ACD��
��2������ACB=62�������BDC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֤����
��ͼ����֪AD��BC��EF��BC����1=��2��

��֤��DG��BA��
֤������AD��BC��EF��BC����֪��
���EFB=��ADB=90�㣨 ��
��EF��AD�� ��
���1=��BAD�� ��
���ߡ�1=��2����֪��
�� ������������
��DG��BA���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���齭����ij���ν�ˮ����B��C��D����������ԭ����ͬ����ͼ������ABC=120�㣬��BCD=80�㣬���CDE=__________�ȣ�

����22�⣩
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com