
【题目】已知:点A、C、B不在同一条直线上,AD∥BE.
(1)如图①,当∠A=48°,∠B=128°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.

【答案】(1)100°(2)2∠AQB+∠C=180°(3)1:2:2
【解析】
(1)过点C作CF∥AD,则CF∥BE,根据平行线的性质可得出∠ACF=∠A、∠BCF=180°∠B,将其代入∠ACB=∠ACF+∠BCF即可求出∠ACB的度数;
(2)过点Q作QM∥AD,则QM∥BE,根据平行线的性质、角平分线的定义可得出∠AQB=![]() (∠CBE∠CAD),结合(1)的结论可得出2∠AQB+∠C=180°;
(∠CBE∠CAD),结合(1)的结论可得出2∠AQB+∠C=180°;
(3)由(2)的结论可得出∠CAD=![]() ∠CBE①,由QP⊥PB可得出∠CAD+∠CBE=180°②,联立①②可求出∠CAD、∠CBE的度数,再结合(1)的结论可得出∠ACB的度数,将其代入∠DAC:∠ACB:∠CBE中可求出结论.
∠CBE①,由QP⊥PB可得出∠CAD+∠CBE=180°②,联立①②可求出∠CAD、∠CBE的度数,再结合(1)的结论可得出∠ACB的度数,将其代入∠DAC:∠ACB:∠CBE中可求出结论.
(1)在图①中,过点C作CF∥AD,则CF∥BE.

∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°∠B,
∴∠ACB=∠ACF+∠BCF=180°(∠B∠A)=120°.
(2)在图②中,过点Q作QM∥AD,则QM∥BE.
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,

∴∠NAD=![]() ∠CAD,∠EBQ=
∠CAD,∠EBQ=![]() ∠CBE,
∠CBE,
∴∠AQB=∠BQM∠AQM=![]() (∠CBE∠CAD).
(∠CBE∠CAD).
∵∠C=180°(∠CBE∠CAD)=180°2∠AQB,
∴2∠AQB+∠C=180°.
(3)∵AC∥QB,
∴∠AQB=∠CAP=![]() ∠CAD,∠ACP=∠PBQ=
∠CAD,∠ACP=∠PBQ=![]() ∠CBE,
∠CBE,
∴∠ACB=180°∠ACP=180°![]() ∠CBE.
∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD=![]() ∠CBE.
∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠ACB=180°(∠CBE∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.


科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD,△BCE,△ACF,请解答下列问题:
(1)求证:四边形AFED是平行四边形;
(2)当△ABC满足 时,四边形AFED是矩形.
当△ABC满足 时,四边形AFED是菱形.
当△ABC满足 时,四边形AFED是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,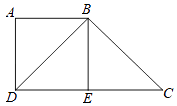
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:
单价/万元 | 工作效率/(只/h) | |
A种型号 | 16 | 4000 |
B种型号 | 14.8 | 3000 |
(1)求购进A,B两种型号的口罩生产线各多少台.
(2)现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2![]() 、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E,F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
(1)若∠A=40°,求∠B的度数;
(2)试说明:DG垂直平分EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com