
【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
【答案】(1)见解析;(2)45°
【解析】
(1)利用三角形内角和证明即可;
(2)利用∠C=20°,∠BAC=110°求出∠ABC,根据BE平分∠ABC求出∠CBE=25°,再根据EF/AD求出∠ADB=∠EFB=110°,最后利用三角形内角和求出结果.
解:(1)∵∠BAD=180°-∠ABC-∠ADB,∠C=180°-∠ABC-∠BAC,
∵∠ADB=∠BAC,
∴∠BAD=∠C;
(2)∵∠C=20°,∠BAC=110°,
∴∠ABC=180°-110°-20°=50°,∠ADB=∠BAC=110°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=25°,
∵AD∥EF,
∴∠ADB=∠EFB=110°,
∴∠BEF=180°-∠CBE-∠BFE=45°.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是______.(添加一个条件即可,不添加其它的点和线).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.

根据图像回答下列问题:
(1)小明家离图书馆的距离是________千米;
(2)小明在图书馆看书的时间为________小时;
(3)小明去图书馆时的速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C,D,B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)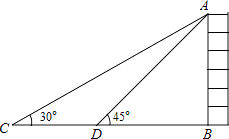
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )
A. ﹣1<a≤0B. 0≤a<1C. ﹣1<a<1D. ﹣2<a<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、C、B不在同一条直线上,AD∥BE.
(1)如图①,当∠A=48°,∠B=128°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小新家、小华家和书店依次在东风大街同一侧(忽略三者与东风大街的距离).小新小华两人同时各自从家出发沿东风大街匀速步行到书店买书,已知小新到达书店用了20分钟,小华的步行速度是40米/分,设小新、小华离小华家的距离分别为y1(米)、y2(米),两人离家后步行的时间为x(分),y1与x的函数图象如图所示,根据图象解决下列问题:
(1)小新的速度为_____米/分,a=_____;并在图中画出y2与x的函数图象
(2)求小新路过小华家后,y1与x之间的函数关系式.
(3)直接写出两人离小华家的距离相等时x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com