
【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
科目:初中数学 来源: 题型:
【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.

(1)∠CAF= °;
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠MON=60°,A、B两点同时从点O出发,点A以每秒x个单位长度沿射线ON匀速运动,点B以每秒y个单位长度沿射线OM匀速运动.

(1)若运动1s时,点A运动的路程比点B运动路程的2倍还多1个单位长度,运动3s时,点A、点B的运动路程之和为12个单位长度,则x=____,y=____;
(2)如图2,点C为△ABO三条内角平分线交点,连接BC、AC,在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由;
(3)如图3,在(2)的条件下,连接OC并延长,与∠ABM的角平分线交于点P,与AB交于点Q.
①试说明∠PBQ=∠ACQ;
②在△BCP中,如果有一个角是另一个角的2倍,请直接写出∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,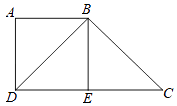
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2![]() 、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com