Question

【题目】已知：如图，四边形ABED是正方形，DB⊥BC，点E为线段DC的中点，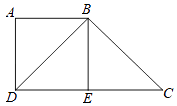

（1）求证：BD2=ADDC．
（2）连接AE，求证：ABCE为平行四边形．

Answer 1

【答案】
（1）解：证明：∵四边形ABED是正方形，

∴∠A=90°，AB=AD，∠ADB=∠ABD=45°，

∵BE⊥CD，点E为线段DC的中点，

∴BD=BC，

∵DB⊥BC，

∴∠BDC=∠C=45°，

∴△ABD∽△DBC，

∴ ，

∴BD2=ADDC；

（2）解：证明：连接AE，

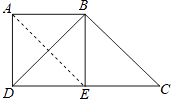
∵四边形ABED是正方形，

∴∠AED=45°，AB∥CD，

∵∠C=45°，

∴∠AED=∠C，

∴AE∥BC，

∴四边形ABCE为平行四边形．

【解析】（1） 由正方形的性质知∠A=90°，AB=AD，∠ADB=∠ABD=45°又由中垂线的性质知BD=BC，进而得出△ABD∽△DBC，由相似三角形对应边成比例得出结论；由正方形的性质得出∠AED=45°，AB∥CD，进而得出∠AED=∠C，故AE∥BC，从而四边形ABCE为平行四边形．
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识，掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．