
【题目】如图1,已知∠MON=60°,A、B两点同时从点O出发,点A以每秒x个单位长度沿射线ON匀速运动,点B以每秒y个单位长度沿射线OM匀速运动.

(1)若运动1s时,点A运动的路程比点B运动路程的2倍还多1个单位长度,运动3s时,点A、点B的运动路程之和为12个单位长度,则x=____,y=____;
(2)如图2,点C为△ABO三条内角平分线交点,连接BC、AC,在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由;
(3)如图3,在(2)的条件下,连接OC并延长,与∠ABM的角平分线交于点P,与AB交于点Q.
①试说明∠PBQ=∠ACQ;
②在△BCP中,如果有一个角是另一个角的2倍,请直接写出∠BAO的度数.
【答案】(1)3,1;(2)![]() 的度数不发生变化,
的度数不发生变化,![]() ;(3)①说明见解析;②
;(3)①说明见解析;②![]() .
.
【解析】
(1)根据“路程![]() 速度
速度![]() 时间”建立一个关于x、y的二元一次方程组,求解即可得;
时间”建立一个关于x、y的二元一次方程组,求解即可得;
(2)先根据三角形的内角和定理可得![]() ,再根据角平分线的定义可得
,再根据角平分线的定义可得![]() ,然后根据三角形的内角和定理即可得;
,然后根据三角形的内角和定理即可得;
(3)①先根据三角形的外角性质可得![]() ,再根据角平行线的定义即可得;
,再根据角平行线的定义即可得;
②先根据角平分线的定义、平角的定义得出![]() ,再根据三角形的外角性质得出
,再根据三角形的外角性质得出![]() ,从而得出
,从而得出![]() ,然后根据直角三角形的性质得出
,然后根据直角三角形的性质得出![]() ,最后根据角的和差、角平分线的定义即可得.
,最后根据角的和差、角平分线的定义即可得.
(1)由题意得:![]()
化简得![]()
解得![]()
故答案为:3,1;
(2)![]() 的度数不发生变化,其值求解如下:
的度数不发生变化,其值求解如下:
由三角形的内角和定理得![]()
![]() 点C为
点C为![]() 三条内角平分线交点,即AC平分
三条内角平分线交点,即AC平分![]() ,BC平分
,BC平分![]()
![]()
![]()
由三角形的内角和定理得![]() ;
;
(3)①由三角形的外角性质得:![]()
![]() 点C为
点C为![]() 三条内角平分线交点,即AC平分
三条内角平分线交点,即AC平分![]() ,OC平分
,OC平分![]()
![]()
![]()
又![]() 是
是![]() 的角平分线
的角平分线
![]()
![]() ;
;
②![]() 是
是![]() 的角平分线,BC平分
的角平分线,BC平分![]()
![]()
![]()
由三角形的外角性质得:![]()
则在![]() 中,如果有一个角是另一个角的2倍,那么一定是
中,如果有一个角是另一个角的2倍,那么一定是![]()
![]()
![]()
![]()
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】“镇康人民想致富,可惜差条二级路”这一啊数瑟小调流传镇康大街小巷.经有关部门批准,龙南二级路已于 2015 年初启动,已知两工程队共同参与某项筑路工程,甲队单独施工一个月完成总工程的![]() ,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:
,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:
(1)那个工程队的施工速度快?
(2)若甲、乙两队同时施工,需多少时间完成整项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.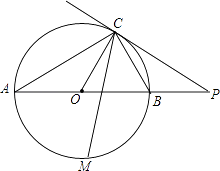
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,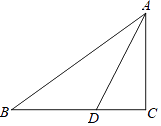
(1)求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)
(2)求证:BC是⊙O切线.
(3)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 . 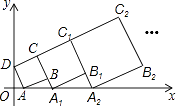
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com