Question

【题目】如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．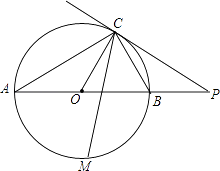

（1）求证：PC是⊙O的切线；
（2）求证：BC= AB；
（3）点M是 的中点，CM交AB于点N，若AB=4，求MNMC的值．

Answer 1

【答案】
（1）解：证明：∵OA=OC，

∴∠A=∠ACO．

又∵∠COB=2∠A，∠COB=2∠PCB，

∴∠A=∠ACO=∠PCB．

又∵AB是⊙O的直径，

∴∠ACO+∠OCB=90°．

∴∠PCB+∠OCB=90°．

即OC⊥CP，

∵OC是⊙O的半径．

∴PC是⊙O的切线．

（2）解：证明：∵AC=PC，

∴∠A=∠P，

∴∠A=∠ACO=∠PCB=∠P．

又∵∠COB=∠A+∠ACO，∠CBO=∠P+∠PCB，

∴∠COB=∠CBO，

∴BC=OC．

∴BC= AB．

（3）解：连接MA，MB，

∵点M是 的中点，

∴ ，

∴∠ACM=∠BCM．

∵∠ACM=∠ABM，

∴∠BCM=∠ABM．

∵∠BMN=∠BMC，

∴△MBN∽△MCB．

∴ ．

∴BM2=MNMC．

又∵AB是⊙O的直径， ，

∴∠AMB=90°，AM=BM．

∵AB=4，

∴BM=2 ．

∴MNMC=BM2=8．

【解析】（1）已知点C在圆上，故只需证明OC与PC垂直即可，根据圆周角定理，得∠PCB+∠OCB=90°．即OC⊥CP，故PC是⊙O的切线；（2）AB事直径，故只需证明BC与半径相等即可；（3）连接MA，MB，由圆周角定理可得∠ACM=∠BCM．进而可证△MBN∽△MCB．故BM2=MNMC．代入数据可得MNMC=BM2=8．