
【题目】如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2![]() 、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
【答案】(1)∠BDC=∠A+∠B+∠C,详见解析;(2)①40;②∠DCE=90°;③70
【解析】
(1)根据题意观察图形连接AD并延长至点F,根据一个三角形的外角等于与它不相邻的两个内角的和可证∠BDC=∠BDF+∠CDF;
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值;
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=![]() (∠ADB+∠AEB)+∠A,易得答案.
(∠ADB+∠AEB)+∠A,易得答案.
③由②方法,进而可得答案.
解:(1)连接AD并延长至点F,
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
∵∠BDC=∠BDF+∠CDF,
∴∠BDC=∠BAD+∠B+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD;
∴∠BDC=∠BAC +∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
∵∠A=50°,∠BXC=90°,
∴∠ABX+∠ACX=90°﹣50°=40°.
故答案是:40;
②由(1)的结论易得∠DBE=∠DAE +∠ADB+∠AEB,∠DCE=∠ADC+∠AEC+∠A
∵∠DAE=50°,∠DBE=130°,
∴∠ADB+∠AEB=80°;
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=![]() ∠ADB,∠AEC=
∠ADB,∠AEC=![]() ∠AEB
∠AEB
∴∠DCE=![]() (∠ADB+∠AEB)+∠A=40°+50°=90°;
(∠ADB+∠AEB)+∠A=40°+50°=90°;
③由②知,∠BG1C=![]() (∠ABD+∠ACD)+ ∠A,
(∠ABD+∠ACD)+ ∠A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°﹣x°,
∴![]() (140﹣x)+x=77,
(140﹣x)+x=77,
∴14﹣![]() x+x=77,
x+x=77,
∴x=70,
∴∠A为70°.
故答案是:70.



科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.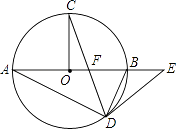
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、C、B不在同一条直线上,AD∥BE.
(1)如图①,当∠A=48°,∠B=128°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,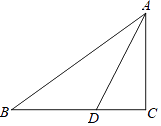
(1)求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)
(2)求证:BC是⊙O切线.
(3)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com