
����Ŀ��ij������72m2��ǽ����Ҫ��ˢ��������4��һ��������ˢһ�죬�����ʣ12m2ǽ��δ��ˢ�ꣻͬ��ʱ���ڰ���6����������ȥ��ˢ����պ�ȫ��ˢ�꣮��֪ÿ��һ�������ȶ�������һ����ˢ3m2ǽ�森��ÿһ��һ������һ���ˢǽ��xm2��
(1)ÿ����������һ���ˢǽ��_____m2(�ú�x��ʽ�ӱ�ʾ)��
(2)��ÿ��һ����������������һ��ֱ��ܷ�ˢ����m2ǽ�棿
(3)ÿ��һ������һ���ʩ������300Ԫ��ÿ����������һ���ʩ������200Ԫ������һ������540m2��ǽ����Ҫ��ˢ��Ҫ��һ���깤��ʩ���ܷ��ò�����10600Ԫ����������Ҫ_____����������(ֱ��д�����)��
���𰸡�(1)(x��3)��(2)15m2��12m2��(3)5��
��������
��1������ÿһ��һ������һ���ˢǽ��xm2��ÿ��һ�������ȶ�������һ����ˢ3m2ǽ�棬����д��ÿ����������һ���ˢǽ��Ϊ(x��3)m2����2������������г�����![]() ��
��![]() ��������⣻��3����������Ҫy����������������Ҫ
��������⣻��3����������Ҫy����������������Ҫ![]() ��һ������������������г�����ʽ�����ɽ������.
��һ������������������г�����ʽ�����ɽ������.
(1) ����ÿһ��һ������һ���ˢǽ��xm2��ÿ��һ�������ȶ�������һ����ˢ3m2ǽ�棬����д��ÿ����������һ���ˢǽ��Ϊ(x��3)m2��
(2)�������з��̣�![]() ��
��![]() ��
��
���x��15��������x��15��ԭ���̵Ľ⣬
��ÿ��һ�������Ͷ�������һ��ֱ��ܷ�ˢ15m2��12m2ǽ�棻
(3) ��������Ҫy����������������Ҫ![]() ��һ��������
��һ��������
�������![]()
���y��5��
��������Ҫ5����������.


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У��е�P��a��b����ʵ��a��b��m��������������ʽ��
2a��3m+1=0��3b��2m��16=0
��1����a=1ʱ����P��x��ľ���Ϊ�� ����
��2������P����x���ϣ���Pƽ�ƺ��Ӧ��ΪP����a+15��b+4�������P��P�������ꣻ
��3����a��4��bʱ����m����С����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ABC��45����CD��AB��D��BEƽ�֡�ABC����BE��AC��E����CD�ཻ�ڵ�F��DH��BC��H��BE��G�����н��ۣ���BD��CD����AD+CF��BD����CE��![]() BF����AE��BG��������ȷ�ĸ����ǣ�������
BF����AE��BG��������ȷ�ĸ����ǣ�������

A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϰ��عˣ���1��������ͼ����![]() �У�
�У�![]() ƽ��
ƽ��![]() ƽ��
ƽ��![]() ����
����![]() _________
_________![]() ��
��

��̽�����죩��![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��2�������м�ͼ����֤��![]() ��
��
��3��������ͼ��![]() ���
���![]() ��ƽ����
��ƽ����![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��
���ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
����![]() ����˵����
����˵����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣�����������AB�۵��ķ����У���һ�����ж�ֽ����������a��b����ƽ�е��ǣ� ��

A. ��ͼ1��չ��������1=��2
B. ��ͼ2��չ��������1=��2����3=��4
C. ��ͼ3�������1=��2
D. ��ͼ4��չ��������CD�۵��������ۺ۵Ľ���ΪO�����OA=OB��OC=OD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���齭����ij���ν�ˮ����B��C��D����������ԭ����ͬ����ͼ������ABC=120�㣬��BCD=80�㣬���CDE=__________�ȣ�

����22�⣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y��kx+2��ͼ����x�ᣬy��ֱ��ڵ�A��B��������������y��![]() x���ڵ�C����֪��C�ĺ�����Ϊ2�����н��ۣ��ٹ���x�ķ���kx+2��0�Ľ�Ϊx��3���ڶ���ֱ��y��kx+2����x��3ʱ��y��0���۶���ֱ��y��kx+2����x��0ʱ��y��2���ܷ�����
x���ڵ�C����֪��C�ĺ�����Ϊ2�����н��ۣ��ٹ���x�ķ���kx+2��0�Ľ�Ϊx��3���ڶ���ֱ��y��kx+2����x��3ʱ��y��0���۶���ֱ��y��kx+2����x��0ʱ��y��2���ܷ�����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��������ȷ���ǣ�������
��������ȷ���ǣ�������

A. �٢ڢ�B. �٢ڢ�C. �٢ۢ�D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y= ![]() ��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F
��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F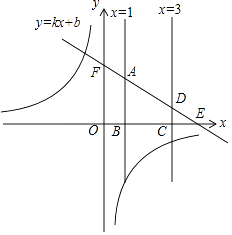
��1���� ![]() =
= ![]() �ҡ�OFE���������
�ҡ�OFE��������� ![]() ʱ�������һ�κ����Ľ���ʽ��
ʱ�������һ�κ����Ľ���ʽ��
��2���ڣ�1���������£����ݺ���ͼ������ʽ ![]() ��kx+b�Ľ⼯��
��kx+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��������������ΪA(-2��3)��B(-6��0)��C(-1��0)
(1) ����ABC������ԭ��O��ת180��������ͼ�Σ���д����A�Ķ�Ӧ��A�� ������________��
(2)����ABC������ԭ��O��ʱ����ת90�㣬
ֱ��д����A�Ķ�Ӧ��A��������___________��
(3)��ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D������___________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com