
����Ŀ����֪����������y= ![]() ��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F
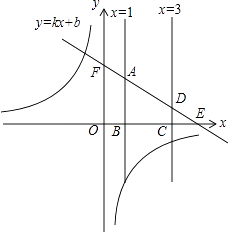
��ͼ���ڵڶ��������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D����A��D���ڵ�һ���ޣ�ֱ��y=kx+b��x�ύ�ڵ�E����y�ύ�ڵ�F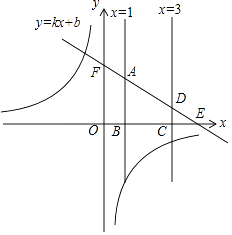
��1���� ![]() =
= ![]() �ҡ�OFE���������
�ҡ�OFE��������� ![]() ʱ�������һ�κ����Ľ���ʽ��
ʱ�������һ�κ����Ľ���ʽ��
��2���ڣ�1���������£����ݺ���ͼ������ʽ ![]() ��kx+b�Ľ⼯��
��kx+b�Ľ⼯��
���𰸡�
��1���⣺������ã� ![]() ��
��
��BC=2��BE=EC+BC��
�� ![]() ��
��
��BE=8��
��OE=9����E��9��0����
�ߵ�F������Ϊ��0��b����
��S��OFE= ![]() ��9��b=
��9��b= ![]() ��
��
���b=3��
��һ�κ���y=kx+3������E��9��0�����ɵ�
k=�� ![]() ��
��
��һ�κ����Ľ���ʽΪy=�� ![]() x+3��
x+3��
��2���⣺� ![]() =��
=�� ![]() x+3��
x+3��
���x1= ![]() ��x2=
��x2= ![]() ��
��
��ֱ��y=kx+b�뷴��������y= ![]() �Ľ�������ĺ�������
�Ľ�������ĺ������� ![]() ��
�� ![]() ��
��
���ʽ ![]() ��kx+b�Ľ⼯Ϊ
��kx+b�Ľ⼯Ϊ ![]() ��x��0��x��
��x��0��x�� ![]() ��
��
����������1����������ó�E������꣬�ٸ���S��OFE= ![]() �����ɵõ�b��ֵ���ٸ���һ�κ���y=kx+b��b��0��������E���ɵ�K��ֵ����2����������������Ľ������꣬�ٸ��ݲ���ʽ
�����ɵõ�b��ֵ���ٸ���һ�κ���y=kx+b��b��0��������E���ɵ�K��ֵ����2����������������Ľ������꣬�ٸ��ݲ���ʽ ![]() ��kx+b�ļ������壬���ɵó����ۡ�
��kx+b�ļ������壬���ɵó����ۡ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���AB�ij�Ϊ3����E��F�ֱ���AD��BC�ϣ�����BE��DF��EF��BD�����ı���BEDF�����Σ���EF=AE+FC�����BC�ij�Ϊ( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������72m2��ǽ����Ҫ��ˢ��������4��һ��������ˢһ�죬�����ʣ12m2ǽ��δ��ˢ�ꣻͬ��ʱ���ڰ���6����������ȥ��ˢ����պ�ȫ��ˢ�꣮��֪ÿ��һ�������ȶ�������һ����ˢ3m2ǽ�森��ÿһ��һ������һ���ˢǽ��xm2��
(1)ÿ����������һ���ˢǽ��_____m2(�ú�x��ʽ�ӱ�ʾ)��
(2)��ÿ��һ����������������һ��ֱ��ܷ�ˢ����m2ǽ�棿
(3)ÿ��һ������һ���ʩ������300Ԫ��ÿ����������һ���ʩ������200Ԫ������һ������540m2��ǽ����Ҫ��ˢ��Ҫ��һ���깤��ʩ���ܷ��ò�����10600Ԫ����������Ҫ_____����������(ֱ��д�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����ij��ѧ���꼶��ͬ��ͬѧ����������꼶ʱ��ѧУ����������࣬���ǽ����������A��B��C�����࣮
��1�������û���״ͼ�����б������г����п��ܵĽ����
��2���������ٴγ�Ϊͬ��ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A1��A2��A3�����ֱ���x���ϣ���B1��B2��B3�����ֱ���ֱ��y��x�ϣ���OA1B1����B1A1A2����B1B2A2����B2A2A3����B2B3A3�������ǵ���ֱ�������Σ����OA1��1�����A2019������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��� ABCDΪ��O���ڽ��ı��ı��Σ���֪��BOD=100�㣬���BCD �Ķ���Ϊ�� ��
A.50��
B.80��
C.100��
D.130��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������ֽ�е�ƽ��չ��ͼ����ֽ֪��������������ϵ�����Ϊ�෴����

![]() ��գ�
��գ� ![]() ��
��![]() ��
��![]() ��
��
![]() �Ȼ��� ����ֵ��
�Ȼ��� ����ֵ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�պ�С������ͼ��ʾ���ܵ��Ͻ���4��50���۷���.�����������У��ܲ��߾������ߵľ���y����λ��m�����ܲ�ʱ��t����λ��s���Ķ�Ӧ��ϵ����ͼ��ʾ.����������ȷ���ǣ� ��


A. ���˴�������ͬʱ������ͬʱ�����յ�
B. С����ȫ�̵�ƽ���ٶȴ���С����ȫ�̵�ƽ���ٶ�
C. С��ǰ15s�ܹ���·�̴���С��ǰ15s�ܹ���·��
D. С���������100m�Ĺ����У���С������2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C����ͼ�б���˵�B�Ķ�Ӧ��B����
(1)�ڸ�������ֽ�л���ƽ�ƺ�ġ�A��B��C����
(2)����BC���ϵĸ���AE��
(3)�������������ǰ廭ͼ����㣺��A��B��C�������Ϊ______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com