
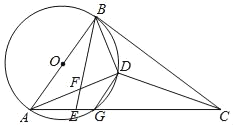
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用三角形内心性质得∠EBD=∠CBD.加上∠DBE=∠BAD,则∠CBD=∠BAD,根据圆周角定理得到∠BDA=90°.然后证明∠ABC=90°.于是根据切线的判定定理可判断BC是⊙O的切线;
(2)连接ED,如图,则∠BED=∠CED,再证明∠EFD=∠EGD,从而可判断△DFE≌△DGE.于是得到DF=DG.
(1)∵点D为△BCE的内心,
∴BD平分∠EBC.
∴∠EBD=∠CBD.
又∵∠DBE=∠BAD,
∴∠CBD=∠BAD.
又∵AB是圆的直径,
∴∠BDA=90°.
在Rt△BAD中,∠BAD+∠ABD=90°,
∴∠CBD+∠ABD=90°,即∠ABC=90°.
∴BC⊥AB.
又∵AB为直径,
∴BC是圆的切线;
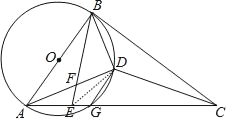
(2)连接ED,如图,则ED平分∠BEC,
∴∠BED=∠CED.
∵∠EFD为△BFD的外角
∴∠EFD=∠ADB+∠EBD=90°+∠EBD,
又∵四边形ABDG为圆的内接四边形,
∴∠EGD=180°﹣∠ABD=180°﹣(90°﹣∠CDB)=90°+∠CDB
又∵∠EBD=∠CBD,
∴∠EFD=∠EGD
又∵ED=ED,
∴△DFE≌△DGE(AAS ).
∴DF=DG.


科目:初中数学 来源: 题型:
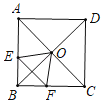
【题目】在边长为![]() 的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为( )
的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为( )
A.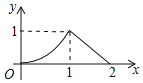 B.
B.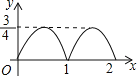
C.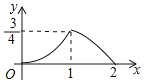 D.
D.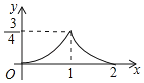
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车起步价是5元(3千米及3千米以内为起步价),以后每增加1千米加收1元,不足1千米按1千米收费.
(1)写出收费y(元)与行驶里程x(千米)之间的函数关系式.
(2)小黄在社会调查活动中,了解到一周内某出租车载客307次,请补全如下条形统计图,并求该出租车这7天运营收入的平均数.
(3)如果出租车1天运营成本是60元,请根据(2)中数据计算出租车司机一个月的收入(以30天计).
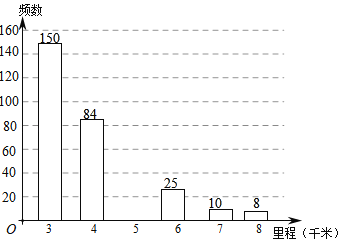
查看答案和解析>>
科目:初中数学 来源: 题型:
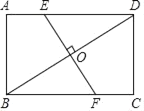
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
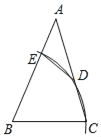
【题目】如图,在△ABC中.以点B为圆心,以BC为半径作弧,分别交AC、AB于点D,E,连接DE,若DE=DC,AE=4.AD=5,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
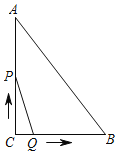
【题目】如图,在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P从点C出发,沿折线CA→AB以3cm/s的速度匀速运动,动点Q从C出发沿CB以1cm/s的速度匀速运动,若动点P、Q同时从点C出发任意一点到达B点时两点都停止运动,则这一过程中,△PCQ的面积S(cm2)与运动时间t(s)之间的关系大致图象是( )
A.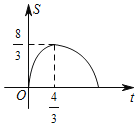 B.
B.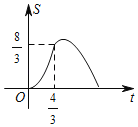
C.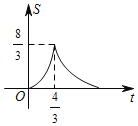 D.
D.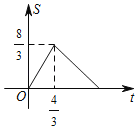
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.
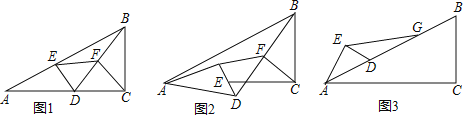
(1)发现问题:线段EF,CF之间的数量关系为_____;∠EFC的度数为_____;
(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;
(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
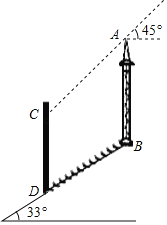
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com