
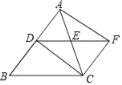
【题目】如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.
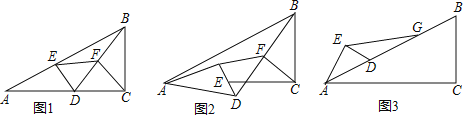
(1)发现问题:线段EF,CF之间的数量关系为_____;∠EFC的度数为_____;
(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;
(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.
【答案】(1)EF=CF,120°;(2)结论成立,见解析;(3)EG=![]() .
.
【解析】
(1)利用直角三角形斜边中线定理及三角形外角性质解决问题即可;(2)结论成立.如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.想办法证明△MFC≌△NEF(SAS),可得结论;(3)如图3中,作EH⊥AB于H.想办法求出EH,HG即可解决问题.
(1)如图1中,
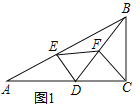
∵DE⊥AB,
∴∠BED=90°,
∵∠BCD=90°,BF=DF,∠A=30°,
∴FE=FB=FD=CF,∠ABC=60°,
∴∠FBE=∠FEB,∠FBC=∠FCB,
∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,
故答案为:EF=CF,120°.
(2)结论成立.
理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.
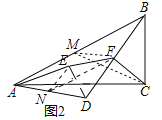
∵BM=MA,BF=FD,
∴MF∥AD,MF=![]() AD,
AD,
∵AN=ND,
∴MF=AN,MF∥AN,
∴四边形MFNA是平行四边形,
∴NF=AM,∠FMA=∠ANF,
在Rt△ADE中,∵AN=ND,∠AED=90°,
∴EN=![]() AD=AN=ND,同理CM=
AD=AN=ND,同理CM=![]() AB=AM=MB,
AB=AM=MB,
在△AEN和△ACM中,
∠AEN=∠EAN,∠MCA=∠MAC,
∵∠MAC=∠EAN,
∴∠AMC=∠ANE,
又∵∠FMA=∠ANF,
∴∠ENF=∠FMC,
在△MFC和△NEF中,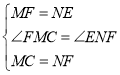 ,
,
∴△MFC≌△NEF(SAS),
∴FE=FC,∠NFE=∠MCF,
∵NF∥AB,
∴∠NFD=∠ABD,
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°
∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.
(3)如图3中,作EH⊥AB于H.
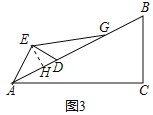
在Rt△ABC中,∵∠BAC=30°,BC=3,
∴AB=2BC=6,
在Rt△AED中,∠DAE=30°,AD=2,
∴DE=![]() AD=1,
AD=1,
在Rt△DEH中,∵∠EDH=60°,DE=1,
∴EH=EDsin60°=![]() ,
,
DH=EDcos60°=![]() ,
,
在Rt△EHG中,EG=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=2![]() ,求ABCD的面积.
,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆P的半径为10,A、B是圆上任意两点,且AB=12,以AB为边作正方ABCD(点D、P在直线AB的两侧),若AB边绕点P旋转一周,则CD边扫过的面积为( ).
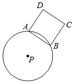
A.0B.36πC.![]() D.6π
D.6π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
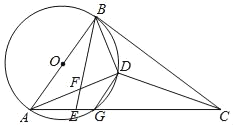
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全真重要,病从口入危害大.良好习惯要养成,食品挑选切注意.”是食品卫生安全歌谣中的一段歌词,某中学针对一些学生不吃正餐,爱吃街边小吃及一些三无小食品,严重危害身体健康的情况,为提高学生们的食品安全意识组织了食品安全教育活动.学校就“是否会根据食品的三无情况来挑选日常食品”的问题在活动前随机抽取一部分学生进行调查,大致有以下五种观点:A:不吃“三无”食品;B:“三无”食品不太安全,可以少吃,但不能多吃;C:看着干净、卫生的食品就可以放心食用;D:高档的,贵的食品都可放心食用;E:不用关注食品的“三无”情况活动后再次调查这部分学生持这几种观点的情况,并将统计结果绘制成如下不完整的统计图(每位同学仅持一种观点).
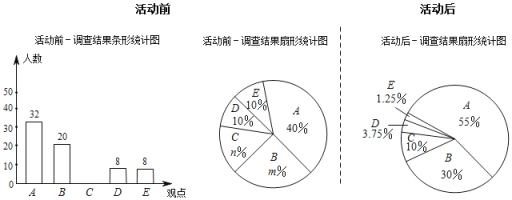
根据以上统计图,解答下列问题:
(1)活动前后,每次接受调查的学生总人数都为_____人,m=_____,n=_____;
(2)请补全活动前的调查结果条形统计图.
(3)若全校共有3200人,请你估计通过这次活动后,还有多少人持E种观点?
(4)根据活动前后的相关数据,说明活动的效果,并提出合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,连接AF、DC.
(1)求证:四边形ADCF是平行四边形;
(2)若AC=BC,判断四边形ADCF的形状,无需说明理由;
(3)若∠ACB=90°,判断四边形ADCF的形状,无需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
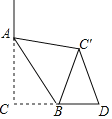
【题目】如图,CD=4,∠C=90°,点B在线段CD上,![]() ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为_____.
,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com