
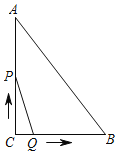
【题目】如图,在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P从点C出发,沿折线CA→AB以3cm/s的速度匀速运动,动点Q从C出发沿CB以1cm/s的速度匀速运动,若动点P、Q同时从点C出发任意一点到达B点时两点都停止运动,则这一过程中,△PCQ的面积S(cm2)与运动时间t(s)之间的关系大致图象是( )
A.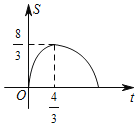 B.
B.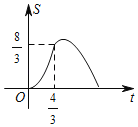
C.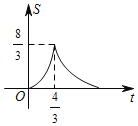 D.
D.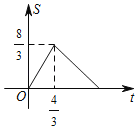
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
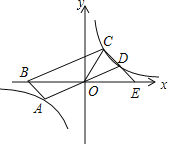
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AD经过O点,A、C、D三点都在反比例函数y=![]() 的图象上,B点在x轴的负半轴上,延长CD交x轴于点E,连接CO.若S平行四边形ABCD=6,则k的值为_____.
的图象上,B点在x轴的负半轴上,延长CD交x轴于点E,连接CO.若S平行四边形ABCD=6,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列语句中,叙述正确的个数为( )
①相等的圆周角所对弧相等;
②同圆等圆中,同弦或等弦所对圆周角相等;
③平分弦的直径垂直于弦;
④等弧所对圆周角相等;
⑤圆的内接平行四边形是矩形;
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
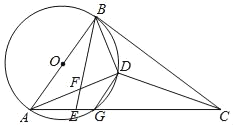
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
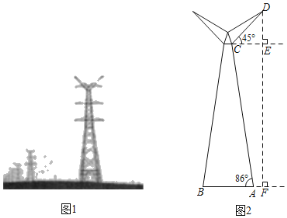
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
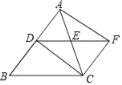
【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,连接AF、DC.
(1)求证:四边形ADCF是平行四边形;
(2)若AC=BC,判断四边形ADCF的形状,无需说明理由;
(3)若∠ACB=90°,判断四边形ADCF的形状,无需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
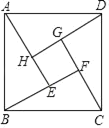
【题目】如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为”赵爽弦图“.已知AE=4,BE=3,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com