
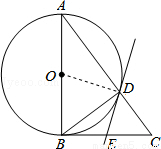
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与边AC交于点D,过点D的直线交BC边于点E,∠BDE=∠A.

(1)证明:DE是⊙O的切线;
(2)若⊙O的半径R=5,tanA= ,求线段CD的长.
,求线段CD的长.
(1)证明见试题解析;(2) .
.
【解析】
(1)连接OD,利用圆周角定理以及等腰三角形的性质得出OD⊥DE,进而得出答案;
(2)得出△BCD∽△ACB,进而利用相似三角形的性质得出CD的长.
试题解析:(1)连接OD.∵OA=OD,∴∠ODA=∠A,又∵∠BDE=∠A,∴∠ODA=∠BDE,∵AB是⊙O直径,∴∠ADB=90°,即∠ODA+∠ODB=90°,∴∠BDE+∠ODB=90°,∴∠ODE=90°,∴OD⊥DE,∴DE与⊙O相切;
(2)∵R=5,∴AB=10,在Rt△ABC中,∵tanA= ,∴BC= AB·tanA=10×
,∴BC= AB·tanA=10×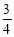 =
=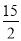 ,∴AC=
,∴AC=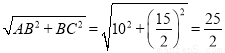 ,∵∠BDC=∠ABC=90°,∠BCD=∠ACB,∴△BCD∽△ACB,
,∵∠BDC=∠ABC=90°,∠BCD=∠ACB,∴△BCD∽△ACB,
∴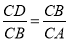 ,∴
,∴ .
.
考点:1.切线的判定;2.勾股定理;3.相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,在△ABC中,BC=2, ,∠ABC=135°,求AC和AB的长.
,∠ABC=135°,求AC和AB的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:填空题
我们规定:线段外一点和这条线段两个端点连线所构成的角叫做这个点对这条线段的视角.如图1,对于线段AB及线段AB外一点C,我们称∠ACB为点C对线段AB的视角.

如图2,在平面直角坐标系 中,已知点D(0,4),E(0,1).
中,已知点D(0,4),E(0,1).
(1)⊙P为过D,E两点的圆, F为⊙P上异于点D,E的一点.
①如果DE为⊙P的直径,那么点F对线段DE的视角∠DFE为_________度;
②如果⊙P的半径为 ,那么点F对线段DE的视角∠DFE为_________度;
,那么点F对线段DE的视角∠DFE为_________度;
(2)点G为x轴正半轴上的一个动点,当点G对线段DE的视角∠DGE最大时,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,点C的坐标为(0,2),动点A以每秒1个单位长的速度从点O出发沿 轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转
轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转 得到线段AB.联结CB.设△ABC的面积为S,运动时间为
得到线段AB.联结CB.设△ABC的面积为S,运动时间为 秒,则下列图象中,能表示S与
秒,则下列图象中,能表示S与 的函数关系的图象大致是( )
的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A,O的对称点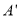 ,
,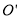 .设∠ABP =α.
.设∠ABP =α.

(1)当α=10°时,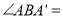 °;
°;
(2)当点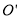 落在
落在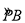 上时,求出
上时,求出 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知反比例函数 (k是常数,且
(k是常数,且 )的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 .
)的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:解答题
将表示下列事件发生的概率的字母标在下图中:

(1)投掷一枚骰子,掷出7点的概率 ;
;
(2)在数学测验中做一道四个选项的选择题(单选题),由于不知道那个是正确选项,现任选一个,做对的概率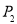 ;
;
(3)袋子中有两个红球,一个黄球,从袋子中任取一球是红球的概率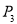 ;
;
(4)太阳每天东升西落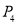 ;
;
(5)在1---100之间,随机抽出一个整数是偶数的概率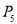 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com