
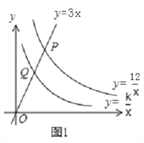
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊжБЯпy=3xЗжБ№гыЫЋЧњЯпy=![]() ЁЂy=
ЁЂy=![]() ЃЈxЃО0ЃЉНЛгкPЁЂQСНЕуЃЌЧвOP=2OQЃЎ
ЃЈxЃО0ЃЉНЛгкPЁЂQСНЕуЃЌЧвOP=2OQЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЎ
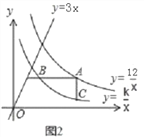
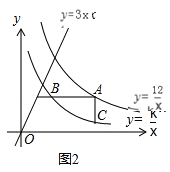
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуAЪЧЫЋЧњЯпy= ![]() ЩЯЕФЖЏЕуЃЌABЁЮxжсЃЌACЁЮyжсЃЌЗжБ№НЛЫЋЧњЯпy=
ЩЯЕФЖЏЕуЃЌABЁЮxжсЃЌACЁЮyжсЃЌЗжБ№НЛЫЋЧњЯпy=![]() ЃЈxЃО0ЃЉгкЕуBЁЂCЃЌСЌНгBCЃЎЧыФуЬНЫїдкЕуAдЫЖЏЙ§ГЬжаЃЌЁїABCЕФУцЛ§ЪЧЗёБфЛЏЃПШєВЛБфЃЌЧыЧѓГіЁїABCЕФУцЛ§ЃЛШєИФБфЃЌЧыЫЕУїРэгЩЃЛ
ЃЈxЃО0ЃЉгкЕуBЁЂCЃЌСЌНгBCЃЎЧыФуЬНЫїдкЕуAдЫЖЏЙ§ГЬжаЃЌЁїABCЕФУцЛ§ЪЧЗёБфЛЏЃПШєВЛБфЃЌЧыЧѓГіЁїABCЕФУцЛ§ЃЛШєИФБфЃЌЧыЫЕУїРэгЩЃЛ
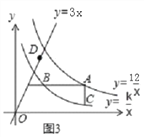
ЃЈ3ЃЉШчЭМ3ЃЌШєЕуDЪЧжБЯпy=3xЩЯЕФвЛЕуЃЌЧыФуНјвЛВНЬНЫїдкЕуAдЫЖЏЙ§ГЬжаЃЌвдЕуAЁЂBЁЂCЁЂDЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓГіДЫЪБЕуAЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉPЃЈ2,6ЃЉ Q(1,3)ЃЌk=3ЃЛЃЈ2ЃЉдкЕуAдЫЖЏЙ§ГЬжаЃЌЁїABCЕФУцЛ§ВЛБфЃЌЪМжеЕШгк![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЕБЕуAЁЂBЁЂCЁЂDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЪБЃЌДЫЪБЕуAЕФзјБъЮЊЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ
ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ![]() ЃЌ6
ЃЌ6![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЯШЧѓГіЕуPЕФзјБъЃЌдйДгЬѕМўOP=2OQГіЗЂЃЌЙЙдьЯрЫЦШ§НЧаЮЃЌЧѓГіQЕузјБъЃЌОЭПЩвдЧѓГіkЕФжЕ.
ЃЈ2ЃЉЩшЕуAЕуЕФзјБъЮЊЃЈa,bЃЉЃЌвзЕУb=![]() ЃЌНсКЯЬѕМўПЩгУaЕФДњЪ§ЪНБэЪОЕуBЃЌЕуCЕФзјБъЃЌНјЖјБэЪОГіЯпЖЮABЃЌACЕФГЄЃЌОЭПЩЫуГіЁїBACЕФУцЛ§ЪЧвЛИіЖЈжЕ.
ЃЌНсКЯЬѕМўПЩгУaЕФДњЪ§ЪНБэЪОЕуBЃЌЕуCЕФзјБъЃЌНјЖјБэЪОГіЯпЖЮABЃЌACЕФГЄЃЌОЭПЩЫуГіЁїBACЕФУцЛ§ЪЧвЛИіЖЈжЕ.
ЃЈ3ЃЉвдЕуAЃЌBЃЌCЃЌDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮПЩЗжГЩСНРрЃКЂйACЮЊЦНааЫФБпаЮЕФвЛБпЃЌЂкACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЃЛШЛКѓРћгУЦНааЫФБпаЮЕФаджЪНЈСЂЙигкaЕФЗНГЬЃЌМДПЩЧѓГіaЕФжЕЃЌДгЖјЧѓГіЕуAЕФзјБъ.
ЃЈ1ЃЉPЃЈ2,6ЃЉ Q(1,3)ЃЌk=3.
ЃЈ2ЃЉШчЭМ2ЃЌ
ЁрSЁїABC=![]() ABAC=
ABAC=![]() ЁС
ЁС![]() ЁС
ЁС![]() .
.
ЁрдкЕуAдЫЖЏЙ§ГЬжаЃЌЁїABCЕФУцЛ§ВЛБфЃЌЪМжеЕШгк![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЂйACЮЊЦНааЫФБпаЮЕФвЛБпЃЌ
ЂёЃЎЕБЕуBдкЕуQЕФгвБпЪБЃЌШчЭМ3ЃЌ
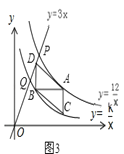
ЁпЫФБпаЮACBDЪЧЦНааЫФБпаЮЃЌЁрACЁЮBDЃЌAC=BDЃЎЁрxD=xB=![]() ЃЎ
ЃЎ
ЁрyD=3xD=![]() ЃЎЁрDB=
ЃЎЁрDB=![]() .
.
ЁпAC=![]() ЃЌЁр
ЃЌЁр![]() =
=![]() ЃЎНтЕУЃКa=ЁР2
ЃЎНтЕУЃКa=ЁР2![]() ЃЎ
ЃЎ
ОМьбщЃКa=ЁР2![]() ЪЧИУЗНГЬЕФНтЃЎЁпaЃО0ЃЌЁрa=2
ЪЧИУЗНГЬЕФНтЃЎЁпaЃО0ЃЌЁрa=2![]() ЃЎЁрb=
ЃЎЁрb=![]() .
.
ЁрЕуAЕФзјБъЮЊЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЂђЃЎЕБЕуBдкЕуQЕФзѓБпЧвЕуCдкЕуQЕФгвБпЪБЃЌШчЭМ4ЃЌ
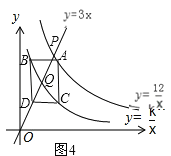
ЁпЫФБпаЮACDBЪЧЦНааЫФБпаЮЃЌЁрACЁЮBDЃЌAC=BDЃЎ
ЁрxD=xB=![]() ЃЎЁрyD=3xD=
ЃЎЁрyD=3xD=![]() ЃЎЁрDB=
ЃЎЁрDB=![]() .
.
ЁпAC=![]() ЃЌЁр
ЃЌЁр![]() =
=![]() ЃЌНтЕУЃКa=ЁР2ЃЎ
ЃЌНтЕУЃКa=ЁР2ЃЎ
ОМьбщЃКa=ЁР2ЪЧИУЗНГЬЕФНтЃЎ
ЁпaЃО0ЃЌЁрa=2ЃЎЁрb=![]() =6ЃЎ
=6ЃЎ
ЁрЕуAЕФзјБъЮЊЃЈ2ЃЌ6ЃЉЃЎ
ЂкACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЃЌ
ДЫЪБЕуBЁЂЕуCЖМдкЕуQЕФзѓБпЃЌШчЭМ5ЃЌ
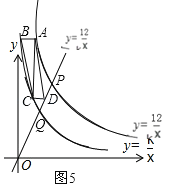
ЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрABЁЮCDЃЌAB=CDЃЎЁрyD=yC=![]() ЃЎЁрxD=
ЃЎЁрxD=![]() ЃЎ
ЃЎ
ЁрCD=![]() ЉaЃЎЁпAB=aЉ
ЉaЃЎЁпAB=aЉ![]() ЃЌЁр
ЃЌЁр![]() =
=![]() ЉaЃЎ
ЉaЃЎ
НтЕУЃКa=ЁР![]() ЃЎ
ЃЎ
ОМьбщЃКa=ЁР![]() ЪЧИУЗНГЬЕФНтЃЎ
ЪЧИУЗНГЬЕФНтЃЎ
ЁпaЃО0ЃЌЁрa=![]() ЃЎЁрb=
ЃЎЁрb=![]() =6
=6![]() ЃЎ
ЃЎ
ЁрЕуAЕФзјБъЮЊЃЈ![]() ЃЌ6
ЃЌ6![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃКЕБЕуAЁЂBЁЂCЁЂDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЪБЃЌДЫЪБЕуAЕФзјБъЮЊЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ
ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ![]() ЃЌ6
ЃЌ6![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
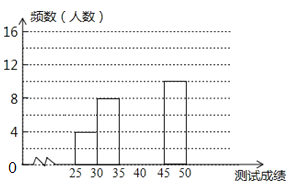
ЁОЬтФПЁПЮЊСЫЬсИпбЇЩњЪщаДККзжЕФФмСІЃЎдіЧПБЃЛЄККзжЕФвтЪЖЃЌЮвЧјОйАьСЫЁАККзжЬ§аДДѓШќЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБЬ§аД50ИіККзжЃЌШєУПе§ШЗЬ§аДГівЛИіККзжЕУ1ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 25ЁмxЃМ30 | 4 |
Ек2зщ | 30ЁмxЃМ35 | 6 |
Ек3зщ | 35ЁмxЃМ40 | 14 |
Ек4зщ | 40ЁмxЃМ45 | a |
Ек5зщ | 45ЁмxЃМ50 | 10 |
ЧыНсКЯЭМБэЭъГЩЯТСаИїЬтЃК
ЃЈ1ЃЉЧѓБэжаaЕФжЕЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєВтЪдГЩМЈВЛЕЭгк40ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
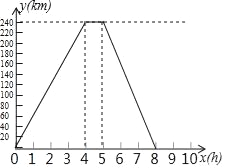
ЁОЬтФПЁПвЛСОЛѕГЕДгAЕидЫЛѕЕН240kmЕФBЕиЃЌаЖЛѕКѓЗЕЛиAЕиЃЌШчЭМжаЪЕЯпЪЧЛѕГЕРыAЕиЕФТЗГЬyЃЈkmЃЉЙигкГіЗЂКѓЕФЪБМфxЃЈhЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЎЛѕГЕГіЗЂЪБЃЌе§гавЛИіздааГЕЦяааЭХдкABжЎМфЃЌОрAЕи40kmДІЃЌвдУПаЁЪБ20kmЕФЫйЖШБМЯђBЕиЃЎ
ЃЈ1ЃЉЛѕГЕШЅBЕиЕФЫйЖШЪЧЁЁ ЁЁЃЌаЖЛѕгУСЫЁЁ ЁЁаЁЪБЃЌЗЕЛиЕФЫйЖШЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓГіздааГЕЦяааЭХОрAЕиЕФТЗГЬyЃЈkmЃЉЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂдкДЫзјБъЯЕжаЛГіЫќЕФЭМЯѓЃЛ
ЃЈ3ЃЉЧѓздааГЕЦяааЭХгыЛѕГЕгУцЯргіЃЌЪЧЛѕГЕГіЗЂКѓМИаЁЪБКѓЃЌздааГЕЦяааЭХЛЙгаЖрдЖЕНДяBЕиЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкжБНЧзјБъЯЕжа,вбжЊЕуE(3,2)дкЫЋЧњЯпy=![]() (x>0)ЩЯЁЃЙ§ЖЏЕуP(t,0)зїxжсЕФДЙЯпЗжБ№гыИУЫЋЧњЯпКЭжБЯпy=
(x>0)ЩЯЁЃЙ§ЖЏЕуP(t,0)зїxжсЕФДЙЯпЗжБ№гыИУЫЋЧњЯпКЭжБЯпy=![]() xНЛгкA.ЁЂBСНЕу,вдЯпЖЮABЮЊЖдНЧЯпзїе§ЗНаЮADBC,ЕБе§ЗНаЮADBCЕФБп(ВЛАќРЈе§ЗНаЮЖЅЕу)ОЙ§ЕуEЪБЃЌдђtЕФжЕЮЊ___.
xНЛгкA.ЁЂBСНЕу,вдЯпЖЮABЮЊЖдНЧЯпзїе§ЗНаЮADBC,ЕБе§ЗНаЮADBCЕФБп(ВЛАќРЈе§ЗНаЮЖЅЕу)ОЙ§ЕуEЪБЃЌдђtЕФжЕЮЊ___.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCдкжБНЧзјБъЯЕжаЃЌ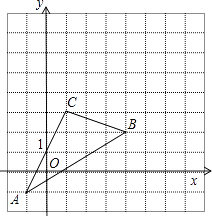
ЃЈ1ЃЉЧыаДГіЁїABCИїЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓГіSЁїABCЃЛ
ЃЈ3ЃЉШєАбЁїABCЯђЩЯЦНвЦ2ИіЕЅЮЛЃЌдйЯђгвЦНвЦ2ИіЕЅЮЛЕУЁїAЁфBЁфCЁфЃЌдкЭМжаЛГіЁїABCБфЛЏЮЛжУЃЌВЂаДГіAЁфЁЂBЁфЁЂCЁфЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁїACDбиADелЕўЃЌЪЙЕУЕуCТфдкаББпABЩЯЕФЕуEДІЃЎ
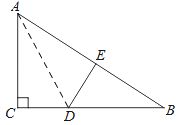
ЃЈ1ЃЉЧѓжЄЃКЁїBDEЁзЁїBACЃЛ
ЃЈ2ЃЉвбжЊAC=6ЃЌBC=8ЃЌЧѓЯпЖЮADЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕР1+2+3+Ё+![]() =
=![]() ЃЌдђ1+2+3+Ё+10ЃН ___________ .
ЃЌдђ1+2+3+Ё+10ЃН ___________ .
[ЮЪЬтЬсГі] ФЧУД ![]() ЕФНсЙћЕШгкЖрЩйФиЃП
ЕФНсЙћЕШгкЖрЩйФиЃП
[дФЖСРэНт] дкЭМ1ЫљЪОЕФШ§НЧаЮЪ§еѓжаЃЌЕк1аадВШІжаЕФЪ§ЮЊ1ЃЌМД12 ЃЛЕк2ааСНИідВШІжаЪ§ЕФКЭЮЊ2+2ЃЌМД22ЃЛ......ЃЛЕкnааnИідВШІжаЪ§ЕФКЭЮЊn+n+![]() nМД n2ЃЛетбљЃЌИУШ§НЧаЮЪ§еѓжаЙВга____ ИідВШІЃЌЫљгадВШІжаЪ§ЕФКЭПЩБэЪОЮЊ_________________ .
nМД n2ЃЛетбљЃЌИУШ§НЧаЮЪ§еѓжаЙВга____ ИідВШІЃЌЫљгадВШІжаЪ§ЕФКЭПЩБэЪОЮЊ_________________ .
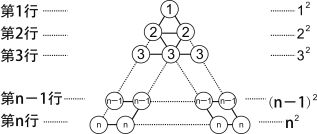
ЭМ1
[ЙцТЩЬНОП] НЋШ§НЧаЮЪ§еѓОСНДЮа§зЊПЩЕУШчЭМ2ЫљЪОЕФШ§НЧаЮЪ§еѓЃЌЙлВьетШ§ИіШ§НЧаЮЪ§еѓИїааЭЌвЛЮЛжУдВШІжаЕФЪ§ЃЈШчЕкnЃ1ааЕФЕквЛИідВШІжаЕФЪ§ЗжБ№ЮЊnЃ1ЃЌ2ЃЌnЃЉЗЂЯжУПИіЮЛжУЩЯШ§ИідВШІжаЕФЪ§ЕФКЭОљЮЊ______________.гЩДЫПЩЕУЃЌетШ§ИіШ§НЧаЮЪ§еѓЫљгадВШІжаЪ§ЕФзмКЭЮЊЃК
3ЃЈ![]() ЃЉЃН_________________.вђДЫЃЌ
ЃЉЃН_________________.вђДЫЃЌ![]() ЃН__________.
ЃН__________.

ЭМ2
[ЮЪЬтНтОі]
ЃЈ1ЃЉ.ИљОнвдЩЯЙцТЩПЩЕУ![]() __________________.
__________________.
ЃЈ2ЃЉ.ЪдМЦЫу ![]() ЃЌЧыаДГіМЦЫуВНжш.
ЃЌЧыаДГіМЦЫуВНжш.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛИідЫЫузАжУЃЌЕБЪфШыжЕЮЊxЪБЃЌЦфЪфГіжЕЮЊyЃЌЧвyЪЧxЕФЖўДЮКЏЪ§ЃЌвбжЊЪфШыжЕЮЊЉ2ЃЌ0ЃЌ1ЪБЃЌЯргІЕФЪфГіжЕЗжБ№ЮЊ5ЃЌЉ3ЃЌЉ4ЃЎ 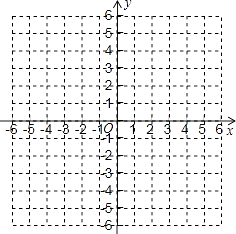
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЫљИјЕФзјБъЯЕжаЛГіетИіЖўДЮКЏЪ§ЕФЭМЯѓЃЌВЂИљОнЭМЯѓаДГіЕБЪфГіжЕyЮЊе§Ъ§ЪБЪфШыжЕxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЙ§ЕуCЕФжБЯпMNЁЮABЃЌDЮЊABБпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭBCЃЌНЛжБЯпMNгкEЃЌДЙзуЮЊFЃЌСЌНгCDЃЌBE.
ЃЈ1ЃЉЧѓжЄЃКCEЃНADЃЛ
ЃЈ2ЃЉЕБDЮЊABжаЕуЪБЃЌЫФБпаЮBECDЪЧЪВУДЬиЪтЫФБпаЮЃПЫЕУїФуЕФРэгЩЃЛ
ЃЈ3ЃЉШєDЮЊABжаЕуЃЌдђЕБЁЯAЕФДѓаЁТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮBECDЪЧе§ЗНаЮЃПЧыЫЕУїФуЕФРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com