
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD. 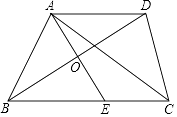
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论.
【答案】
(1)证明:∵BD平分∠ABC,AE⊥BD,
∴AO=EO
(2)平行四边形,
证明:∵AD∥BC,
∴∠ADB=∠ABD,∴
AD=BD,
在△ABO和△BBO中, 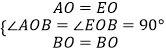 ,
,
∴△ABO≌△BBO,
∴AB=BE,
∴AD=BE,
∵AE=CE,
∴AE=EC,
∴四边形AECD是平行四边形
【解析】(1)由“三线合一”定理即可得到结论;(2)由AD∥BC,BD平分∠ABC,得到∠ADB=∠ABD,由等腰三角形的判定得到AD=BD,根据“SAS”定理证得△ABO≌△BBO,由全等三角形的性质有AB=BE,于是AD=BE,进而得到AE=EC,根据平行四边形的判定即可得到结论.
【考点精析】关于本题考查的菱形的判定方法,需要了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ON 平分∠AOC,OM平分∠BOC
(1)若∠AOB=90°∠AOC=50°,则∠MON= °;
(2)若∠AOB=80°∠AOC=60°,则∠MON= °;
(3)探索:∠MON与∠AOB有何关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,菱形ABCD中,AB=10cm,BD=12cm,对角线AC与BD相交于点O,直线MN以1cm/s从点D出发,沿DB方向匀速运动,运动过程中始终保持MN⊥BD,垂足是点P,过点P作PQ⊥BC,交BC于点Q.(0<t<6) 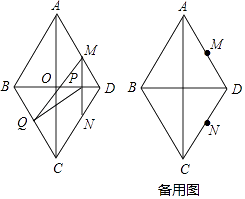
(1)求线段PQ的长;(用含t的代数式表示)
(2)设△MQP的面积为y(单位:cm2),求y与t的函数关系式;
(3)是否存在某时刻t,使线段MQ恰好经过点O?若存在求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2 . 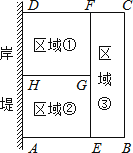
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com