
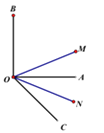
【题目】如图, ON 平分∠AOC,OM平分∠BOC
(1)若∠AOB=90°∠AOC=50°,则∠MON= °;
(2)若∠AOB=80°∠AOC=60°,则∠MON= °;
(3)探索:∠MON与∠AOB有何关系?请说明理由.

【答案】(1)45°;(2)40°;(3)∠MON=![]() ∠AOB,理由见解析.
∠AOB,理由见解析.
【解析】
(1)(2)问根据角平分线均可计算出.
(3)可根据前问的思路求出∠MON与∠AOB关系.
(1)45°;∵∠AOB=90°,∠AOC=50°
∴∠BOC=50°+90°=140°
∵OM平分∠BOC.∴∠MOC=70°
∵ON 平分∠AOC, ∠AOC=50°
∴∠NOA=∠NOC=25°
∴∠MON=∠MOC-∠NOC=70°-25°=45°.
(2)40°;∵∠AOB=80°,∠AOC=60°
∴∠BOC=50°+90°=140°
∵OM平分∠BOC.∴∠MOC=70°
∵ON 平分∠AOC, ∠AOC=60°
∴∠NOA=∠NOC=30°
∴∠MON=∠MOC-∠NOC=70°-30°=40°.
(3)∠MON=![]() ∠AOB,
∠AOB,
∵OM,ON分别平分∠BOC和∠AOC
∴∠MOC=![]() ∠BOC, ∠NOC=
∠BOC, ∠NOC=![]() ∠AOC
∠AOC
∴∠MON=∠MOC- ∠NOC =![]() ∠BOC-
∠BOC-![]() ∠AOC =
∠AOC =![]() (∠BOC-∠AOC) =
(∠BOC-∠AOC) =![]() ∠AOB
∠AOB


科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).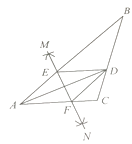
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() (
(![]() )上,则k的值为( )
)上,则k的值为( )

A. 4 B. ﹣2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( ) 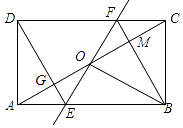
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD. 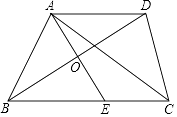
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作 ![]() .过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 . 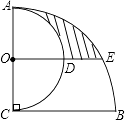
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com