练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知AB是⊙O的直径，BC为弦，过圆心O作OD⊥BC交弧BC于点D，连接DC，若∠DCB=32°，则∠BAC= ．

    【答案】64°
    【解析】解：∵∠BOD与∠BCD为 所对的圆心角和圆周角， ∴∠BOD=2∠BCD=64°，
    ∵AB为直径，∴AC⊥BC，
    又∵OD⊥BC，∴AC∥OD，
    ∴∠BAC=∠BOD=64°，
    所以答案是：64°．
    【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图， ON 平分∠AOC，OM平分∠BOC

    (1)若∠AOB=90°∠AOC=50°，则∠MON= °；

    (2)若∠AOB=80°∠AOC=60°，则∠MON= °；

    (3)探索：∠MON与∠AOB有何关系？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程
    （1）解方程组：
    （2）已知关于x的一元二次方程x2+2x﹣m=1有实数根，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中的位置如图所示．

    （1）在图中画出△ABC与关于y轴对称的图形△A1B1C1，并写出顶点A1、B1、C1的坐标；

    （2）若将线段A1C1平移后得到线段A2C2，且A2（a，2），C2（-2，b），求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD∥BC，要是四边形ABCD成为平行四边形，则应增加的条件是（ ）
    A.AB=CD
    B.∠BAD=∠DCB
    C.AC=BD
    D.∠ABC+∠BAD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线AB：y=-x-b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．

    （1）求点B的坐标；

    （2）求直线BC的解析式；

    （3）直线EF：y=2x-k（k≠0）交AB于E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S△EBD=S△FBD？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2 ．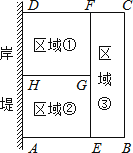

    （1）求y与x之间的函数关系式，并注明自变量x的取值范围；
    （2）x为何值时，y有最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b﹣1）x+c的图象可能是（　　）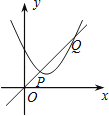

    A.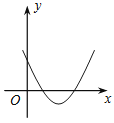
    B.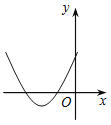
    C.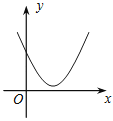
    D.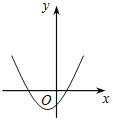

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，四边形ABCO为正方形，A点坐标为（0，2），点P为x轴负半轴上一动点，以AP为直角作等腰直角三角形APD，∠APD=90°（点D落在第四象限）

    （1）当点P的坐标为（﹣1，0）时，求点D的坐标；
    （2）点P在移动的过程中，点D是否在直线y=x﹣2上？请说明理由；
    （3）连接OB交AD于点G，求证：AG=DG．

    查看答案和解析>>

    同步练习册答案