
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
【答案】(1) B点坐标为:(0,6).(2) y=3x+6.(3) k=-2.4
【解析】
试题(1)将点A(6,0)代入直线AB的解析式,可得b的值,继而可得点B的坐标;
(2)设BC的解析式是y=ax+c,根据B点的坐标,求出C点坐标,把B,C点的坐标分别代入求出a和c的值即可;
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°,有题目的条件证明△NFD≌△EDM,进而得到FN=ME,联立直线AB:y=-x-b和y=2x-k求出交点E和F的纵坐标,再利用等底等高的三角形面积相等即可求出k的值;
试题解析:(1)将点A(6,0)代入直线AB解析式可得:0=-6-b,
解得:b=-6,
∴直线AB 解析式为y=-x+6,
∴B点坐标为:(0,6).
(2)∵OB:OC=3:1,
∴OC=2,
∴点C的坐标为(-2,0),
设BC的解析式是y=ax+c,代入得;![]() ,
,
解得:![]() ,
,
∴直线BC的解析式是:y=3x+6.
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°.
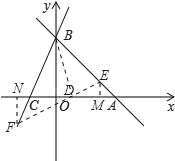
∵S△EBD=S△FBD,
∴DE=DF.
又∵∠NDF=∠EDM,
∴△NFD≌△EDM,
∴FN=ME,
联立得![]() ,
,
解得:yE=-![]() k+4,
k+4,
联立![]() ,
,
解得:yF=-3k-12,
∵FN=-yF,ME=yE,
∴3k+12=-![]() k+4,
k+4,
∴k=-2.4;
当k=-2.4时,存在直线EF:y=2x-2.4,使得S△EBD=S△FBD.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用y= ![]() x2﹣
x2﹣ ![]() x+3表示
x+3表示 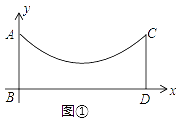
(1)求这条绳子最低点离地面的距离;
(2)现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑(如图②),已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.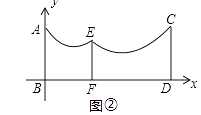
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD= ![]() .
. 
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点的门票价格如下表:
购票人数(单位人) | 1﹣50 | 51﹣100 | 100以上 |
每人门票价(单位元) | 80 | 75 | 70 |
某旅行社计划帶甲、乙两个旅行团共100多人计划去游览该景点,其中甲旅行团人数少于50人,乙旅行团人数有50 多人但不足100人,如果两旅行团都以各自团体为单位单独购票,则一共支付7965元;如果两旅行团联合起来作为一个团体购票,则只管花费7210元.间两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜和甜瓜是新疆特色水果,小明的妈妈先购买了2千克西瓜和3千克甜瓜,共花费9元;后又购买了1千克西瓜和2千克甜瓜,共花费5.5元.(每次两种水果的售价都不变)
(1)求两种水果的售价分别是每千克多少元?
(2)如果还需购买两种水果共12千克,要求甜瓜的数量不少于西瓜数量的两倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com