
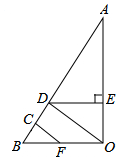
 如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,
如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,分析 先由垂直的定义可得:∠AED=∠AOB=90°,然后根据同位角相等,两条直线平行,可得:DE∥BO,进而根据两直线平行,内错角相等,可得∠EDO=∠BOD,然后由等量代换可得:∠BOD=∠CFB,进而由同位角相等,两条直线平行可得:CF∥DO.
解答 证明:∵DE⊥AO,BO⊥AO,
∴∠AED=∠AOB=90°,
∴DE∥BO(同位角相等,两条直线平行),
∴∠EDO=∠BOD(两直线平行,内错角相等),
∵∠EDO=∠CFB,
∴∠BOD=∠CFB,
∴CF∥DO(同位角相等,两条直线平行).
点评 本题考查了平行线的性质和判定的应用,能运用平行线的性质和判定进行推理是解此题的关键,难度适中.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a2-(2a-b+5c)=3a2-2a+b-5c | B. | 5x2+(-2x+y)-(3z-u)=5x2-2x+y-3z+u | ||
| C. | 2m2-3(m-1)=2m2-3m-1 | D. | -(2x-y)-(-x2+y2)=-2x+y+x2-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com