
如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,AB2=AP•AD.
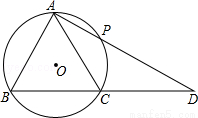
(1)求证:AB=AC;
(2)如果∠ABC=60°,⊙O的半径为1,且P为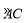 的中点,求AD的长.
的中点,求AD的长.
(1)证明见试题解析;(2)3.
【解析】
试题分析:(1)根据AB2=AP•AD,可以连接BP,构造相似三角形.根据相似三角形的性质得到∠APB=∠ABD,再根据圆周角定理得到∠APB=∠ACB,即∠ABC=∠ACB,从而由等角对等边证明结论;
(2)因为有一个角是60°的等腰三角形是等边三角形,发现等边三角形ABC,再根据点P为弧的中点,连接BP,发现30°的直角三角形,且BP是直径,从而求得AP的长,AB的长.再根据已知中的条件求得AD的长.
试题解析:(1)连接BP,∵AB2=AP•AD,∴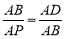 ,又∵∠BAD=∠PAB,∴△ABD∽△APB,
,又∵∠BAD=∠PAB,∴△ABD∽△APB,
∵∠ABC=∠APB,∠APB=∠ACB,∴∠ABC=∠ACB,∴AB=AC;
(2)由(1)知AB=AC,∵∠ABC=60°,∴△ABC为等边三角形,∴∠BAC=60°,
∵P为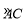 的中点,∴∠ABP=∠PAC=
的中点,∴∠ABP=∠PAC=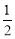 ∠ABC=30°,∴∠BAP=∠BAC+∠PAC=90°,∴BP为直径,∴BP过圆心O,∴BP=2,∴AP=
∠ABC=30°,∴∠BAP=∠BAC+∠PAC=90°,∴BP为直径,∴BP过圆心O,∴BP=2,∴AP=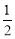 BP=1,∴
BP=1,∴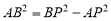 ,∵AB2=AP•AD,∴AD=
,∵AB2=AP•AD,∴AD=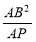 =3.
=3.
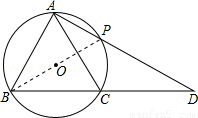
考点:1.圆周角定理;2.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年浙江省九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分)某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量 与销售单价
与销售单价 之间的关系可以近似地看作一次函数:
之间的关系可以近似地看作一次函数: ,物价部门规定这种笔记本每本的销售单价不得高于18元.
,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元?
(2)该文具店这种笔记本每月获得利润为 元,求每月获得的利润
元,求每月获得的利润 元与销售单价
元与销售单价 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级10月月考数学试卷(解析版) 题型:选择题
把抛物线 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )。
向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )。
A.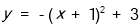
B.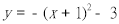
C.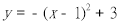
D.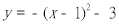
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省景洪市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
若A点的坐标是(1,3),则点A关于原点对称的点M的坐标是__________
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省日照市莒县北五校九年级上学期12月联考数学试卷(解析版) 题型:选择题
若⊙O的半径长是4cm,圆外一点A与⊙O上各点的最远距离是12cm,则自A点所引⊙O的切线长为( )
A.16cm B.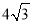 cm C.
cm C.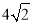 cm D.
cm D.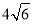 cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com