
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
【答案】详见解析.
【解析】试题分析:(1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论;
(3)利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
试题解析:
(1)解:令a=3,b=4则c=5,写出一个“勾系一元二次方程”:3x+5![]() x+4=0;
x+4=0;
(2)证明:
∵△=(![]() c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
∴关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
(3)代入x=1得a![]() c+b=0,∴a+b=
c+b=0,∴a+b=![]() c.
c.
由四边形ACDE的周长是![]() 得a+b+a+b+
得a+b+a+b+![]() c=
c=![]() ,
,
∴2(a+b)+![]() c=
c=![]() ,2
,2![]() c+
c+![]() c=
c=![]() ,3
,3![]() c=
c=![]() ,c=2,a+b=2
,c=2,a+b=2![]() ,
,
∴2ab=(a+b)(a+b)=(a+b)(c)=84=4,
∴ab=2,
∴△ABC面积=![]()


科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是_______米,小明在书店停留了______分钟.
(2)本次上学途中,小明一共行驶了______米;骑车速度最快是_______米/分. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举办科技比赛,某校参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图如图
(1)该校参加机器人比赛的人数是_____人;“航模”所在扇形的圆心角度数是________°;
(2)补全条形统计图;
(3)从全区参加科技比赛选手中随机抽取80人,其中有16人获奖.今年全区参加科技比赛人数共有3215人,请你估算全区参加科技比赛的获奖人数约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2 ![]() .
. 
(1)求证:BD是⊙O的切线;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:

根据以上信息,下列判断错误的是( )
A. 其中的D型帐篷占帐篷总数的10%
B. 单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C. 单独生产A型帐篷与单独生产D型帐篷的天数相等
D. 单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC =9cm,CB = 6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB =![]() cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足AC![]() BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E. 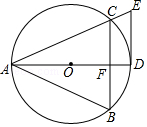
(1)求证:DE∥BC;
(2)若DF=n,∠BAC=2a,写出求CE长的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com