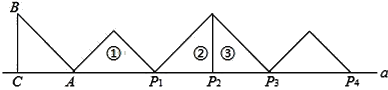
[题目]如图.等腰Rt△ABC中.∠ACB=90°.AC=BC=1.且AC边在直线a上.将△ABC绕点A顺时针旋转到位置①可得到点P1.此时AP1=,将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2.此时AP2=+1,将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时.AP3=+2-按此规律继续旋转.直至得到点为止.则= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=；将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2，此时AP2=+1；将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时，AP3=+2…按此规律继续旋转，直至得到点为止，则=________．

【答案】

【解析】试题解析：AP1=，AP2=1+，AP3=2+；

AP4=2+2；AP5=3+2；AP6=4+2；

AP7=4+3；AP8=5+3；AP9=6+3；

∵2016=3×672，

∴AP2013=（2013-671）+671=1342+671，

∴AP2014=1342+671+=1342+672，

∴AP2015=1342+672+1=1343+672，

∴AP2016=1343+672+1=1344+672，

故答案为：1344+672．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某地下车库出口处安装了“两段式栏杆”，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图所示的位置，其中AB⊥BC，EF∥BC，∠AEF=135°，AB=AE=1.3米，那么适合该地下车库的车辆限高标志牌为（栏杆宽度忽略不计．参考数据：≈1.4）（　　）

A.
B.
C.
D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，数轴的单位长度为1，如果P，Q表示的数互为相反数，那么图中的4个点中，哪一个点表示的数的平方值最大（　　）

A. P B. R C. Q D. T

查看答案和解析>>

科目：初中数学 来源： 题型：

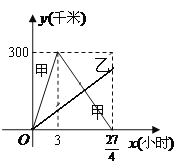
【题目】已知：甲、乙两车分别从相距300千米的 A,B两地同时出发相向而行，其中甲到 B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．

（1）求甲车离出发地的距离 y（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

（2）当它们行驶到与各自出发地的距离相等时，用了小时，求乙车离出发地的距离 y（千米）与行驶时间 x（小时）之间的函数关系式；

（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=交于A（1，3）和B（﹣3，﹣1）两点．
观察图象可知：
①当x=﹣3或1时，y1=y2；
②当﹣3＜x＜0或x＞1时，y1＞y2 ，即通过观察函数的图象，可以得到不等式ax+b＞的解集．
有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．

下面是他的探究过程，请将（2）、（3）、（4）补充完整：
（1）将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x2+4x﹣1＞；
当x＜0时，原不等式可以转化为x2+4x﹣1＜；
（2）构造函数，画出图象
设y3=x2+4x﹣1，y4= ，在同一坐标系中分别画出这两个函数的图象．
双曲线y4=如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）
（3）确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为；
（4）借助图象，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集为．